(文)(本小题满分12分)
已知函数 在
在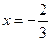 与
与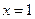 时都取得极值
时都取得极值
(1)求 的值与函数
的值与函数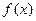 的单调区间
的单调区间
(2)若对 ,不等式
,不等式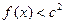 恒成立,求
恒成立,求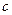 的取值范围。
的取值范围。
统计某区的高考成绩,在总数为3000人的考生中,省重点中学毕业生有300人,区重点中学毕业生有900人,普通中学毕业生有1700人,其他考生有100人.从中抽取一个容量为300的样本进行分析,各类考生要分别抽取多少人?
一条流水线生产某种产品,每天都可生产128件这种产品,我们要对一周内生产的这种产品作抽样检验,方法是抽取这一周内每天下午2点到2点半之间下线的8件产品作检验.这里采用了哪种抽取样本的方法?
写出用二分法求方程x3-x-1=0在区间[1,1.5]上的一个解的算法(误差不超过0.001),并画出相应的程序框图及程序.
我国古代数学家张邱建编《张邱建算经》中记有有趣的数学问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一凡百钱,买鸡百只,问鸡翁、母、雏各几何?”你能用程序解决这个问题吗?
我国《算经十书》之一《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?答曰:二十三.”你能用程序解决这个问题吗?