(本小题12分)
随机调查某社区80个人,以研究这一社区居民在20:00-22:00时间段的休闲方式与性别有关系,得到下面的数据表:
| 休闲方式 性别 |
看电视 |
看书 |
合计 |
| 男 |
10 |
50 |
60 |
| 女 |
10 |
10 |
20 |
| 合计 |
20 |
60 |
80 |
(1)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量
,求的分布列和期望;
(2)根据以上数据,能否有99%的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
参考公式: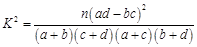 
,其中
参考数据:
 |
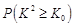0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
 |
2.072 |
2.706 |
3.841 |
5.042 |
6.635 |
两条直线l1：(m＋3)x＋2y＝5－3m，l2：4x＋(5＋m)y＝16，分别求满足下列条件的m的值．
(1) l1与l2相交；
(2) l1与l2平行；
(3) l1与l2重合；
(4) l1与l2垂直．
如图所示,在底面为直角梯形的四棱锥P
ABCD中,AD∥BC,PD⊥平面ABCD,AD=1,AB=
,BC=4.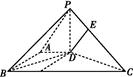
(1)求证:BD⊥PC;
(2)求直线AB与平面PDC所成的角;
(3)设点E在棱PC上,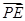
=λ
,若DE∥平面PAB,求λ的值.
如图所示,四棱锥P
ABCD的底面为正方形,侧棱PA⊥底面ABCD,且PA=AD=2,E,F,H分别是线段PA,PD,AB的中点.
(1)求证:PB∥平面EFH;
(2)求证:PD⊥平面AHF.
如图所示,已知三棱柱ABC
A1B1C1,
(1)若M、N分别是AB,A1C的中点,求证:MN∥平面BCC1B1;
(2)若三棱柱ABCA1B1C1的各棱长均为2,∠B1BA=∠B1BC=60°,P为线段B1B上的动点,当PA+PC最小时,求证:B1B⊥平面APC.
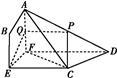
如图所示,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=4,AB=2,点E、F分别在BC、AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABEF⊥平面EFDC,设AD中点为P.
(1)当E为BC中点时,求证:CP∥平面ABEF;
(2)设BE=x,问当x为何值时,三棱锥A
CDF的体积有最大值?并求出这个最大值.