(本题满分12分)
已知数列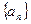 的各项都为正数,
的各项都为正数, ,前
,前 项和
项和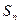 满足
满足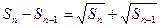 (
(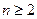 ).
).
(Ⅰ)求数列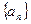 的通项公式;
的通项公式;
(Ⅱ)令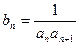 (
(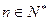 ),数列
),数列 的前
的前 项和为
项和为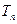 ,若
,若 对任意正整数
对任意正整数 都成立,求实数
都成立,求实数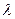 的取值范围.
的取值范围.
已知函数

(1)判断 的奇偶性并证明;
的奇偶性并证明;
(2)若 的定义域为[
的定义域为[ ](
]( ),判断
),判断 在定义域上的增减性,并加以证明;
在定义域上的增减性,并加以证明;
(3)若 ,使
,使 的值域为[
的值域为[ ]的定义域区间[
]的定义域区间[ ](
]( )是否存在?若存在,求出[
)是否存在?若存在,求出[ ],若不存在,请说明理由.
],若不存在,请说明理由.
(本小题14分)根据市场调查,某商品在最近的20天内的价格 与时间
与时间 满足关系
满足关系 {
{ ,销售量
,销售量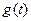 与时间
与时间 满足关系
满足关系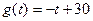 ,
, ,设商品的日销售额为
,设商品的日销售额为 (销售量与价格之积).
(销售量与价格之积).
(1)求商品的日销售额 的解析式;
的解析式;
(2)求商品的日销售额 的最大值.
的最大值.
(本题满分14分,每小题各7分)计算下列各式
(Ⅰ)
(Ⅱ) 
(本小题14分) (1) 证明函数 f(x)= 在
在 上是增函数;
上是增函数;
⑵求 在
在 上的值域。
上的值域。
(本小题12分)已知
⑴求 的值;⑵判断
的值;⑵判断 的奇偶性。
的奇偶性。