(本题满分12分)
已知函数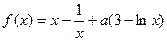 (
(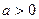 ).
).
(Ⅰ)若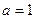 ,求
,求 在
在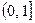 上的最大值;
上的最大值;
(Ⅱ)若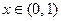 ,求
,求 的单调区间.
的单调区间.
某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出x (x∈ )名员工从事第三产业,调整后他们平均每人每年创造利润为
)名员工从事第三产业,调整后他们平均每人每年创造利润为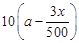 万元(a>0),剩下的员工平均每人每年创造的利润可以提高0.2x%.
万元(a>0),剩下的员工平均每人每年创造的利润可以提高0.2x%.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)在(1)的条件下,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a的取值范围是多少?
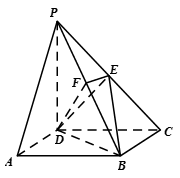
如图,在四棱锥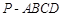 中,底面
中,底面 是矩形,侧棱PD⊥底面
是矩形,侧棱PD⊥底面 ,
,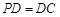 ,
,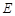 是
是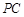 的中点,作
的中点,作 ⊥
⊥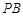 交
交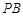 于点
于点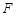 .
.
(1)证明: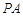 ∥平面
∥平面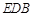 ;
;
(2)证明: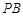 ⊥平面
⊥平面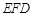 .
.
已知函数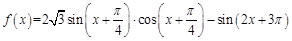 .
.
(1)求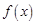 的最小正周期;
的最小正周期;
(2)若将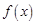 的图像向左平移
的图像向左平移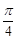 个单位,得到函数
个单位,得到函数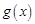 的图像,
的图像,
求函数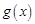 在区间
在区间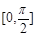 上的最大值和最小值.
上的最大值和最小值.
已知数列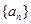 是等差数列,且
是等差数列,且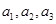 是
是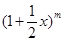 展开式的前三项的系数.
展开式的前三项的系数.
(1)求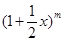 展开式的中间项;
展开式的中间项;
(2)当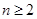 时,试比较
时,试比较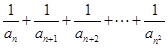 与
与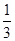 的大小.
的大小.
(本小题满分10分)袋中装有大小相同的黑球和白球共9个,从中任取2个都是白球的概率为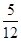 .现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取1个球,取出的球不放回,直到其中有一人取到白球时终止.用X表示取球终止时取球的总次数.
.现甲、乙两人从袋中轮流摸球,甲先取,乙后取,然后甲再取 ,每次摸取1个球,取出的球不放回,直到其中有一人取到白球时终止.用X表示取球终止时取球的总次数.
(1)求袋中原有白球的个数;
(2)求随机变量X的概率分布及数学期望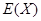 .
.