(本小题满分12分)
一缉私艇发现在方位角45°方向,距离12n mile的海面上有一走私船在以10n mile/h的速度沿方位角为105°方向逃窜,若缉私艇的速度为14n mile/h,缉私艇沿方位角45°+α的方向追去,若要在最短的时间内追上该走私船,求追缉所需时间和α角的正弦.(注:方位角是指指北方向按顺时针方向旋转形成的角)
【改编题】(本大题满分13分)设函数 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ)  时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)函数 是
是 的导函数,求函数
的导函数,求函数 在区间
在区间 上的最小值.
上的最小值.
(Ⅲ)函数 在区间
在区间 内有零点,证明:
内有零点,证明: .
.
(本小题共13分)如图所示,在正方体 中,
中, 分别是棱
分别是棱 的中点.
的中点.
(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)证明: //平面
//平面 ;
;
(Ⅲ)若正方体棱长为1,求四面体 的体积.
的体积.
(本小题满分12分)从某校高三年级800名学生中随机抽取50名测量身高.据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果分成八组得到的频率分布直方图如下: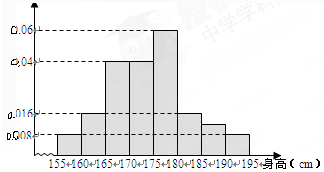
(1)试估计这所学校高三年级800名学生中身高在180cm以上(含180cm)的人数为多少;
(2)在样本中,若学校决定身高在185cm以上的学生中随机抽取2名学生接受某军校考官进行面试,求:身高在190cm以上的学生中至少有一名学生接受面试的概率.
(本小题共12分)设数列 的前
的前 项和为
项和为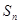 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足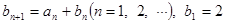 ,求数列
,求数列 的通项公式.
的通项公式.
(本小题满分12分)已知函数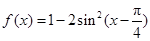 ,x∈R .
,x∈R .
(Ⅰ)求函数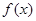 的最小正周期;
的最小正周期;
(Ⅱ)判断函数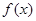 在区间
在区间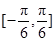 上是否为增函数?并说明理由.
上是否为增函数?并说明理由.