(本小题共13分)如图所示,在正方体 中,
中, 分别是棱
分别是棱 的中点.
的中点.
(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)证明: //平面
//平面 ;
;
(Ⅲ)若正方体棱长为1,求四面体 的体积.
的体积.
(本小题满分12分)某单位组织4个部门的职工旅游,规定每个部门只能在韶山、 衡山、张家界3个景区中任选一个,假设各部门选择每个景区是等可能的.
衡山、张家界3个景区中任选一个,假设各部门选择每个景区是等可能的.
(1)是3个景区都有部门选择的概率是;
(2)求恰有2个景区有部门选择的概率
(本小题满分12分)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为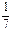 .现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取,
.现有甲、乙两人从袋中轮流摸取1个球,甲先取,乙后取,然后甲再取, ,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求:
,取后不放回,直到两人中有一人取到白球时即终止,每个球在每一次被取出的机会是等可能的.求:
(1)则袋中原有白球的个数;
(2)取球2次终止的概率;
(3)甲取到白球的概率
(本小题满分12分)已知8支球队中有3支弱队,以抽签方式将这8支球队分为A、B两组,每组4支.求:
(1)A、B两组中有一组恰有两支弱队的概率;
(2)A组中至少有两支弱队的概率.
(本小题满分12分)甲、乙两人各进行一次射击,如果两人击中目标的概率都是0.6,计算:
(1)两人都击中目标的概率;
(2)其中恰有一人击中目标的概率;
(3)至少有一人击中目标的概率.
(本小题满分10分)一名学生在军训中练习射击项目,他射击一次,命中目标的概率是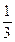 ,若连续射击6次,且各次射击是否命中目标相互之间没有影响.
,若连续射击6次,且各次射击是否命中目标相互之间没有影响.
(1)求这名学生在第3次射击时,首次命中目标的概率;
(2)求这名学生在射击过程中,恰好命中目标3次的概率.