（本题满分
分）为了解高一学生的体
能情况,某校抽取部分学生进行一分钟跳
绳次数的测试，将所得数据整理、分组后，
画出频率分布直方图(如图).图中从左到右
各小长方形面积之比为
.
若第二组的频数为
.
(1) 求第二组的频率是多少？样本容量是
多少？
（2）若次数在
以上（含次）为达标，试估计该学校全体高一学生的达标率是多少？
(12分)给定两个命题，p：对任意实数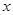
都有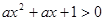
恒成立；q：关于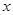的方程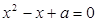
有实数根；若
为真，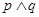
为假，求实数
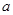的取值范围．
（本小题满分14分）已知数列{an}中，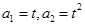
（t>0且t≠1）．若
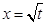是函数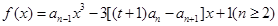
的一个极值点．
（Ⅰ）证明数列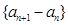
是等比数列，并求数列
的通项公式；
（Ⅱ）记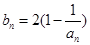
，当t=2时，数列
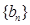的前n项和为Sn，求使Sn>2008的n的最小值；
（Ⅲ）当t=2时，求证：对于任意的正整数n，有 
。
（本小题满分14分）设函数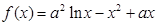
，
;
（Ⅰ）求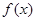
的单调递增区间；
（Ⅱ）若
，求使≤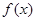
对x∈[1，e]恒成立的实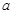
的值。
（注：e为自然对数的底数）
（本小题满分12分）椭圆的两个焦点分别为F1(0,-2
)，F2(0,2)，离心率e =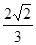
。（Ⅰ）求椭圆方程；（Ⅱ）一条不与坐标轴平行的直线l与椭圆交于不同的两点M、N，且线段MN中点的横坐标为-
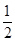，求直线l倾斜角的取值范围。
（本小题满分14分） 已知函数
（Ⅰ）求它的最小正周期T;
（Ⅱ）若
，求
的值；
（Ⅲ）求
的单调增区间．