(本小题满分13分)
某市4997名学生参加高中数学会考,得分均在60分
以上,现从中随机抽取一个容量为500的样本,制成
如图a所示的频率分布直方图.
(Ⅰ)由频率分布直方图可知本次会考的数学平均分为
81分.请估计该市得分在区间 的人数;
的人数;
(Ⅱ)如图b所示茎叶图是某班男女各4名学生的得分情况,
现用简单随机抽样的方法,从这8名学生中,抽取男
女生各一人,求女生得分不低于男生得分的概率.

 (第4题 图a) |
已知向量a=(sinX, ),b=(cosX,﹣1)
),b=(cosX,﹣1)
(1) 当a∥b时,求2cos2X-sin2X的值
(2)求f(x)=(a+b)·b的值域
F1,F2是双曲线的左右焦点,P是双曲线上一点,且∠F1PF2=600,S△PF1 F2=12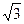
又离心率为2,求双曲线方程。
如图,四棱锥P—ABCD的底面ABCD是边长为1的菱形,∠BCD﹦60°,E是CD中点,
PA⊥底面ABCD,PA=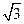
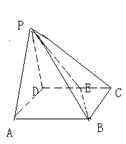
(1)证明:平面PBE⊥平面PAB
(2)求二面角A—BE—P的大小。
数列﹛ ﹜中,
﹜中, =
=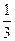 ,前n项和
,前n项和 满足
满足 +1-
+1- =(
=(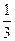 )n+1 (n
)n+1 (n N*
N* )
)
(1)求数列﹛ ﹜的通项公式
﹜的通项公式 以及前n项和
以及前n项和
(2)若 ,t(
,t( +
+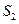 ), 3(
), 3(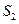 +
+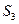 )成等差数列,求实数t的值。
)成等差数列,求实数t的值。
已知0<X<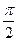 ,
,
化简lg(cosX·tanX﹢1-2sin2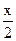 )﹢lg〔
)﹢lg〔 cos(x﹣
cos(x﹣ )〕﹣lg (1+sin2x)
)〕﹣lg (1+sin2x)