（本小题满分12分）
已知椭圆的中心在坐标原点
，焦点在
轴上，椭圆的短轴端点和焦点所组成的四边形为正方形，短轴长为2．
（1）求椭圆的方程；
（2）设直线
过
且与椭圆相交于A，B两点，当P是AB的中点时，求直线的方程．
在锐角△ABC中，角A、B、C所对的边长分别为a、b、c.向量m＝(1，cosB)，n＝(sinB，－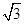
)，且m⊥n.
(1)求角B的大小；
(2)若△ABC面积为10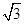，b＝7，求此三角形周长．
若sinα＝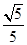
，sinβ＝
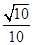，且α、β均为锐角，求α＋β的值．
已知△ABC的角A、B、C所对的边分别是a、b、c，设向量m＝(a，b)，n＝(sinB，sinA)，p＝(b－2，a－2)．
(1)若m∥n，求证：△ABC为等腰三角形；
(2)若m⊥p，边长c＝2，角C＝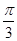
，求△ABC的面积．
已知向量m＝
与n＝(3，sinA＋
cosA)共线，其中A是△ABC的内角．
(1)求角A的大小；
(2)若BC＝2，求△ABC面积S的最大值，并判断S取得最大值时△ABC的形状．
在△ABC中，角A，B，C的对边分别为a，b，c，C＝
，a＝5，△ABC的面积为10
.
(1)求b，c的值；
(2)求cos
的值．