对于给定数列 ,如果存在实常数
,如果存在实常数 使得
使得 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 是 “线性数列”.
是 “线性数列”.
(1)若 ,
, ,
, ,数列
,数列 、
、 是否为“线性数列”?若是,指出它对应的实常数
是否为“线性数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列 是“线性数列”,则数列
是“线性数列”,则数列 也是“线性数列”;
也是“线性数列”;
(3)若数列 满足
满足 ,
, ,
, 为常数.求数列
为常数.求数列 前
前 项的和.
项的和.
(本小题满分10分)已知角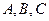 为
为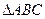 的三个内角,其对边分别为
的三个内角,其对边分别为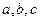 ,若向量
,若向量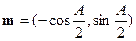 ,
,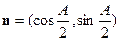 ,
,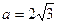 ,且
,且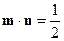 .
.
(1)若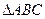 的面积
的面积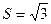 ,求bc的值.
,求bc的值.
(2)求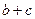 的取值范
的取值范 围.
围.
(1)求动点P的轨迹C的方程;
(2)设M、N是直线l上的两个点,点E是点F关于原点的对称点,若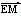 ·
·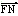 =0,
=0,
求 | MN | 的最小值。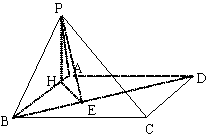
(1)a的值;
(2)函数y=f (x) 的单调区间;
工作,办公室里只有一部电话机,设经该机打进的电话是打给甲、乙、丙的概率依次为 、
、 、
、 。若在一段时间内打进三个电话,且各个电话相互独立。
。若在一段时间内打进三个电话,且各个电话相互独立。
求:(1)这三个电话是打给同一个人的概率。
(2)这三个电话中恰有两个是打给甲的概率。
AD=2,PA=2,PD=2 ,∠PAB=60°。
,∠PAB=60°。
(1)证明:AD⊥平面PAB;
(2)求异面直线PC与AD所成的角的大小;
(3)求二面角P-BD-A的大小。