已知函数 ,
,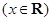 .
.
(1)证明:函数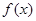 在区间
在区间 上为增函数,并指出函数
上为增函数,并指出函数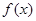 在区间
在区间 上的单调性.
上的单调性.
(2)若函数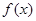 的图像与直线
的图像与直线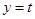 有两个不同的交点
有两个不同的交点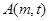 ,
, ,其中
,其中 ,求
,求 关于
关于 的函数关系式.
的函数关系式.
(3)求 的取值范围.
的取值范围.
某学校为了解高三年级学生寒假期间的学习情况,抽取甲、乙两班,调查这两个班的学生在寒假期间每天平均学习的时间(单位:小时),统计结果绘成频率分布直方图(如图).已知甲、乙两班学生人数相同,甲班学生每天平均学习时间在区间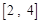 的有8人.
的有8人.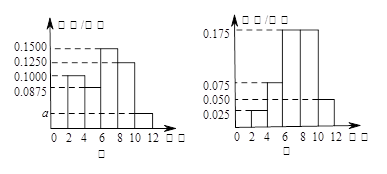
(1)求直方图中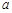 的值及甲班学生每天平均学习时间在区间
的值及甲班学生每天平均学习时间在区间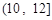 的人数;
的人数;
(2)从甲、乙两个班每天平均学习时间大于10个小时的学生中任取4人参加测试,设4人中甲班学生的人数为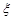 ,求
,求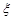 的分布列和数学期望.
的分布列和数学期望.
在 中,
中,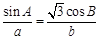 .
.
(1)求角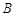 的值;
的值;
(2)如果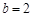 ,求
,求 面积的最大值.
面积的最大值.
已知椭圆 ,过点
,过点 且离心率为
且离心率为 .
.
求椭圆 的方程;
的方程;
已知 是椭圆
是椭圆 的左右顶点,动点
的左右顶点,动点 满足
满足 ,连接
,连接 角椭圆于点
角椭圆于点 ,在
,在 轴上是否存在异于点
轴上是否存在异于点 的定点
的定点 ,使得以
,使得以 为直径的圆经过直线
为直径的圆经过直线 和直线
和直线 的交点,若存在,求出
的交点,若存在,求出 点,若不存在,说明理由.
点,若不存在,说明理由.
如图,底面 是边长为2的菱形,且
是边长为2的菱形,且 ,以
,以 与
与 为底面分别作相同的正三棱锥
为底面分别作相同的正三棱锥 与
与 ,且
,且 .
.
(1)求证: 平面
平面 ;
;
(2)求多面体 的体积.
的体积.
已知函数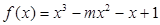 ,其中
,其中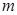 为实数.
为实数.
(1)当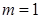 时,求函数
时,求函数 在区间
在区间 上的最大值和最小值;
上的最大值和最小值;
(2)若对一切的实数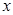 ,有
,有 恒成立,其中
恒成立,其中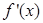 为
为 的导函数,求实数
的导函数,求实数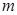 的取值范围.
的取值范围.