已知椭圆 ,过点
,过点 且离心率为
且离心率为 .
.
求椭圆 的方程;
的方程;
已知 是椭圆
是椭圆 的左右顶点,动点
的左右顶点,动点 满足
满足 ,连接
,连接 角椭圆于点
角椭圆于点 ,在
,在 轴上是否存在异于点
轴上是否存在异于点 的定点
的定点 ,使得以
,使得以 为直径的圆经过直线
为直径的圆经过直线 和直线
和直线 的交点,若存在,求出
的交点,若存在,求出 点,若不存在,说明理由.
点,若不存在,说明理由.
已知等差数列 的前n项和为
的前n项和为 ,首项
,首项 ,公差
,公差 ,且
,且 成等比数列。
成等比数列。
(1)求数列 的通项公式及
的通项公式及 ;
;
(2)记 =
= +
+ +
+ +…+
+…+ ,
,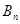 =
= +
+ 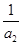 +
+ +… +
+… +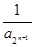 ,
,
当n≥2时,试比较 与
与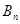 的大小。
的大小。
设函数 .
.
(1)求函数 的单调区间和极值;
的单调区间和极值;
(2)若关于x的方程 有三个不同实根,求实数
有三个不同实根,求实数 的取值范围;
的取值范围;
(3)已知当 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。
已知函数 在
在 处取得极值,过点
处取得极值,过点 作曲线
作曲线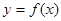 的切线
的切线 ,(1)求此切线
,(1)求此切线 的方程.(2)求切线
的方程.(2)求切线 与函数
与函数 的图象围成的平面图形的面积。
的图象围成的平面图形的面积。
某商场从生产厂家以每件20元购进一批商品,若该商品零售价定为p元,则销量Q(单位:件)与零售价p(单位:元)有如下关系: .问该商品售价定为多少元时毛利润L最大,并求最大毛利润(毛利润=销售收入-进货支出)。
.问该商品售价定为多少元时毛利润L最大,并求最大毛利润(毛利润=销售收入-进货支出)。
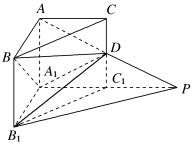
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=AA1=1.D是棱CC1上的中点,P是AD的延长线与A1C1的延长线的交点.
(1)求二面角A-A1D-B的平面角的余弦值;
(2)求点C到平面B1DP的距离.