已知命题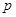 :“关于
:“关于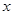 ,
,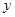 的方程
的方程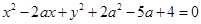 表示圆(
表示圆(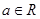 )”,命题
)”,命题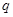 :“
:“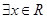 ,使得
,使得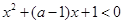 (
(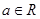 )”.
)”.
(1)若命题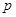 为真命题,求实数
为真命题,求实数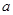 的取值范围;
的取值范围;
(2)若命题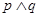 为假命题,求实数
为假命题,求实数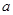 的取值范围.
的取值范围.
(本小题满分10分)已知函数
(1)试求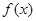 的值域;
的值域;
(2)设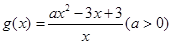 ,若对
,若对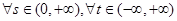 恒有
恒有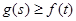 成立,试求实数
成立,试求实数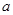 的取值氛围。
的取值氛围。
(本小题满分12分)设函数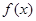 的定义域为R,当
的定义域为R,当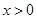 时,
时,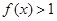 ,且对任意
,且对任意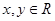 ,都有
,都有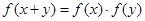 ,且
,且 。
。
(1)求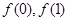 的值;
的值;
(2)证明: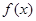 在R上为单调递增函数;
在R上为单调递增函数;
(3)若有不等式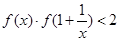 成立,求
成立,求 的取值范围。
的取值范围。
(本小题满分12分)对于定义域为D的函数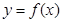 ,若同时满足下列条件:①
,若同时满足下列条件:①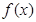 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[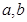 ]
] ,使
,使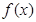 在[
在[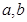 ]上的值域为[
]上的值域为[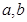 ];那么把
];那么把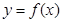 (
(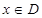 )叫闭函数。(1)求闭函数
)叫闭函数。(1)求闭函数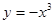 符合条件②的区间[
符合条件②的区间[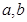 ];
];
(2)判断函数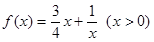 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)判断函数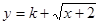 是否为闭函数?若是闭函数,求实数
是否为闭函数?若是闭函数,求实数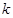 的取值范围。
的取值范围。
(12分)已知定义域为 的单调函数
的单调函数 且
且 图关于点
图关于点 对称,当
对称,当 时,
时, .
.
(1)求 的解析式;
的解析式;
(2)若对任意的 ,不等式
,不等式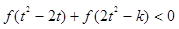 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)函数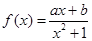 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.
(1)求实数 的值.(2)用定义证明
的值.(2)用定义证明 在
在 上是增函数;
上是增函数;
(3)写出 的单调减区间,并判断
的单调减区间,并判断 有无最大值或最小值?如有,写出最大值或最小值(无需说明理由).
有无最大值或最小值?如有,写出最大值或最小值(无需说明理由).