( 本题满分15分)
本题满分15分)
已知偶函 数
数 满足:当
满足:当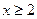 时,
时,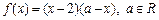 ,当
,当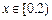 时,
时,
(1) 求当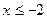 时,
时,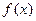 的表达式;
的表达式;
(2) 若直线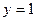 与函数
与函数 的图象恰好有两个公共点,求实数
的图象恰好有两个公共点,求实数 的取值范围。
的取值范围。 (3) 试讨论当实数
(3) 试讨论当实数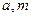 满足什么条件时,函数
满足什么条件时,函数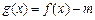 有4个零点且这4个零点从小到大依次成等差数列。
有4个零点且这4个零点从小到大依次成等差数列。
已知三棱锥P-ABC中,PA⊥面ABC,AB⊥AC,PA=AC=½AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.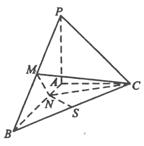
(Ⅰ)证明:CM⊥SN;
(Ⅱ)求SN与平面CMN所成角的大小。
已知动圆M与圆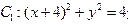 外切,圆
外切,圆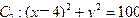 内切
内切
求动圆圆心M 的轨迹方程。
已知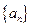 为等差数列,且
为等差数列,且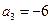 ,
,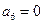 。
。
(Ⅰ)求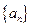 的通项公式;
的通项公式;
(Ⅱ)若等比数列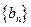 满足
满足 ,
,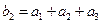 ,求
,求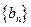 的前n项和公式。
的前n项和公式。
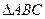 的面积是30,内角
的面积是30,内角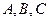 所对边长分别为
所对边长分别为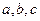 ,
, 。
。
(Ⅰ)求 ;
;
(Ⅱ)若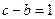 ,求
,求 的值。
的值。
为了迎接2010年在广州举办的亚运会,我市某体校计划举办一次宣传活动,届时将在运动场的一块空地ABCD(如图)上摆放花坛,已知运动场的园林处(P点)有一批鲜花,今要把这批鲜花沿道路PA或PB送到空地ABCD中去,且PA="200" m,PB="300" m,∠APB=60°.
(1)试求A、B两点间的距离;
(2)能否在空地ABCD中确定一条界线,使位于界线一侧的点,沿道路PA送花较近;而另一侧的点,沿道路PB送花较近?如果能,请说出这条界线是一条什么曲线,并求出其方程.