已知方向向量为 的直线
的直线 过点
过点 和椭圆C:
和椭圆C: 
 的焦点
的焦点 ,且椭圆C的中心关于直线
,且椭圆C的中心关于直线 的对称点在椭圆的右准线上, 直线
的对称点在椭圆的右准线上, 直线 过点
过点 交椭圆C于M、N两点.
交椭圆C于M、N两点.
(1)求椭圆C的方程;
(2)若设 是椭圆C的右焦点,若
是椭圆C的右焦点,若 ,求直线
,求直线 的方程;
的方程;
(3)设 (
( 为坐标原点),当直线
为坐标原点),当直线 绕点
绕点 转动时,求
转动时,求 的取值范围.
的取值范围.
在等差数列 中,
中, ,
, 、
、 、
、 成等比数列,求数列
成等比数列,求数列 的前n项和
的前n项和 .
.
已知函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
((本小题满分12分)
设函数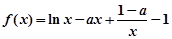 .
.
(Ⅰ)当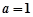 时,过原点的直线与函数
时,过原点的直线与函数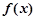 的图象相切于点P,求点P的坐标;
的图象相切于点P,求点P的坐标;
(Ⅱ)当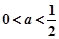 时,求函数
时,求函数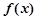 的单调区间;
的单调区间;
(Ⅲ)当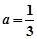 时,设函数
时,设函数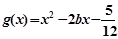 ,若对于
,若对于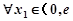 ],
],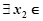 [0,1]
[0,1]
使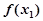 ≥
≥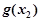 成立,求实数b的取值范围.(
成立,求实数b的取值范围.(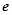 是自然对数的底,
是自然对数的底,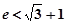 )
)
(.(本小题满分12分)
如图,焦距为2的椭圆E的两个顶点分别为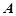 和
和 ,且
,且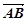 与
与 共线.
共线.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)若直线 与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
((本小题满分12分)
数列 各项均为正数,其前
各项均为正数,其前 项和为
项和为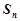 ,且满足
,且满足 .
.
(Ⅰ)求证数列 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)设 , 求数列
, 求数列 的前n项和
的前n项和 ,并求使
,并求使 对所
对所
有的 都成立的最大正整数m的值.
都成立的最大正整数m的值.