(.(本小题满分12分)
如图,焦距为2的椭圆E的两个顶点分别为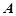 和
和 ,且
,且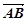 与
与 共线.
共线.
(Ⅰ)求椭圆E的标准方程;
(Ⅱ)若直线 与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
与椭圆E有两个不同的交点P和Q,且原点O总在以PQ为直径的圆的内部,求实数m的取值范围.
已知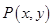 为函数
为函数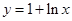 图象上一点,O为坐标原点,记直线
图象上一点,O为坐标原点,记直线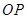 的斜率
的斜率 .
.
(1)若函数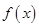 在区间
在区间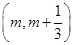
 上存在极值,求实数m的取值范围;
上存在极值,求实数m的取值范围;
(2)设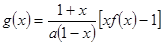 ,若对任意
,若对任意 恒有
恒有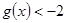 ,求实数
,求实数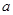 的取值范围.
的取值范围.
已知椭圆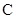 :
: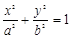 (
(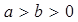 )的右焦点
)的右焦点 ,右顶点
,右顶点 ,且
,且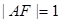 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若动直线 :
: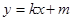 与椭圆
与椭圆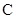 有且只有一个交点
有且只有一个交点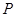 ,且与直线
,且与直线 交于点
交于点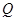 ,问:是否存在一个定点
,问:是否存在一个定点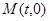 ,使得
,使得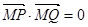 .若存在,求出点
.若存在,求出点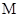 坐标;若不存在,说明理由.
坐标;若不存在,说明理由.
如右图,在底面为平行四边形的四棱柱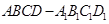 中,
中,
 底面
底面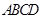 ,
,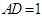 ,
,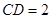 ,
,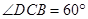 .
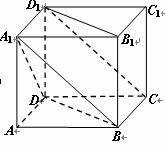
.
(1)求证:平面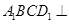 平面
平面 ;
;
(2)若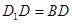 ,求四棱锥
,求四棱锥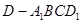 的体积.
的体积.
某学校制定学校发展规划时,对现有教师进行年龄状况和接受教育程度(学历)的调查,其结果(人数分布)如表:
| 学历 |
35岁以下 |
35至50岁 |
50岁以上 |
| 本科 |
80 |
30 |
20 |
| 研究生 |
x |
20 |
y |
(1)用分层抽样的方法在35至50岁年龄段的教师中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有l人的学历为研究生的概率;
(2)在该校教师中按年龄状况用分层抽样的方法抽取N个人,其中35岁以下48人,50岁以上10人,再从这N个人中随机抽取l人,此人的年龄为50岁以上的概率为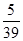 ,求x、y的值.
,求x、y的值.
已知函数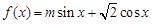 ,
,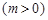 的最大值为2.
的最大值为2.
(1)求函数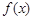 在
在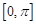 上的值域;
上的值域;
(2)已知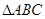 外接圆半径
外接圆半径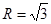 ,
,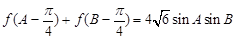 ,角
,角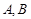 所对的边分别是
所对的边分别是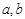 ,求
,求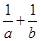 的值.
的值.