已知函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
已知圆C的方程为 ,直线
,直线 .
.
(1)求 的取值范围;
的取值范围;
(2)若圆 与直线
与直线 交于P、Q两点,且以PQ为直径的圆恰过坐标原点,求实数
交于P、Q两点,且以PQ为直径的圆恰过坐标原点,求实数 的值.
的值.
在直角坐标系xOy中,圆C: ,圆心为C,圆C与直线
,圆心为C,圆C与直线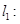
 的一个交点的横坐标为2.
的一个交点的横坐标为2.
(1)求圆C的标准方程;
(2)直线 与
与 垂直,且与圆C交于不同两点A、B,若
垂直,且与圆C交于不同两点A、B,若 ,求直线
,求直线 的方程.
的方程.
点 到
到 的距离是点
的距离是点 到
到 的距离的
的距离的 倍.
倍.
(1)求点 的轨迹方程;
的轨迹方程;
(2)点 与点
与点 关于点
关于点 对称,点
对称,点 ,求
,求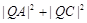 的最大值和最小值.
的最大值和最小值.
(3)若过 的直线从左向右依次交第(2)问中
的直线从左向右依次交第(2)问中 的轨迹于不同两点
的轨迹于不同两点 ,
, ,
,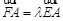 ,判断
,判断 的取值范围并证明.
的取值范围并证明.
已知圆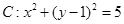 ,直线
,直线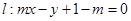
(1)求证:对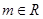 ,直线
,直线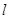 与圆
与圆 总有两个不同的交点A、B;
总有两个不同的交点A、B;
(2)求弦AB的中点M的轨迹方程,并说明其轨迹是什么曲线;
如图,在四棱锥P ABCD中,侧面PAD⊥底面ABCD,侧棱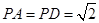 ,
, ,底面
,底面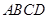 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD, 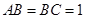 ,O为AD中点.
,O为AD中点.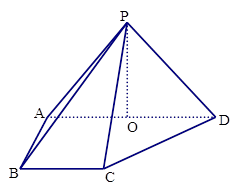
(1)求直线 与平面
与平面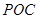 所成角的余弦值;
所成角的余弦值;
(2)求 点到平面
点到平面 的距离;
的距离;
(3)线段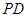 上是否存在一点
上是否存在一点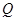 ,使得二面角
,使得二面角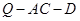 的余弦值为
的余弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.