点 到
到 的距离是点
的距离是点 到
到 的距离的
的距离的 倍.
倍.
(1)求点 的轨迹方程;
的轨迹方程;
(2)点 与点
与点 关于点
关于点 对称,点
对称,点 ,求
,求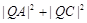 的最大值和最小值.
的最大值和最小值.
(3)若过 的直线从左向右依次交第(2)问中
的直线从左向右依次交第(2)问中 的轨迹于不同两点
的轨迹于不同两点 ,
, ,
,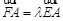 ,判断
,判断 的取值范围并证明.
的取值范围并证明.
(本题11分)
如图,在多面体ABCDE中,AE⊥面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,F为CD中点. (1)求证:EF⊥面BCD;
(2)求面CDE与面ABDE所成的二面角的余弦值.(3)求B点到面ECD的距离
(本题10分)
现有6名翻译,其中 只通
只通 晓法语,
晓法语,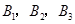 只通晓英语,
只通晓英语,
(Ⅰ)从中选出通晓法语、英语的翻译各1名,组成一个小组.求 被选中且
被选中且 不被选中的概率
不被选中的概率
(II)从6人中任意选三人,求法语、英语翻译都有的概率。
(本题10分)
一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如下图).
(1)直方图中a的值为多少?
(2) 要再用分层抽样方法抽出80人作进一 步调查,则在
步调查,则在 (元)月收入段应抽出的人数为多少人。
(元)月收入段应抽出的人数为多少人。
(本题10分)
如图,在正四棱柱ABCD—A1B1C1D1中,AA1= ,AB=1,E是DD1的中点。
,AB=1,E是DD1的中点。
(I)求证:B1D⊥AE;
(II)求证:BD1 ||平面EAC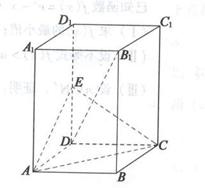
(本题8分)
已知命题 :“x2-x-6<0” ,命题
:“x2-x-6<0” ,命题 :“ x2 >1”,若命题“p且q”为真,求x的范围
:“ x2 >1”,若命题“p且q”为真,求x的范围