某学校的三个学生社团的人数分布如下表（每名学生只能参加一个社团）：
| |
围棋社 |
舞蹈社 |
拳击社 |
| 男生 |
5 |
10 |
28 |
| 女生 |
15 |
30 |
m |
学校要对这三个社团的活动效果进行抽样调查，按分层抽样的方法从三个社团成员中抽取18人，结果拳击社被抽出了6人.
（Ⅰ）求拳击社女生有多少人；
（Ⅱ）从围棋社指定的3名男生和2名女生中随机选出2人参加围棋比赛，求这两名同学是一名男生和一名女生的概率.
已知函数
.
(1) 试判断函数
在
上单调性并证明你的结论；
(2) 若
恒成立, 求整数
的最大值；
(3) 求证：
.
若椭圆C：
的离心率e为
, 且椭圆C的一个焦点与抛物线y2＝－12x的焦点重合．
(1) 求椭圆C的方程；
(2) 设点M(2,0), 点Q是椭圆上一点, 当|MQ|最小时, 试求点Q的坐标；
(3) 设P(m,0)为椭圆C长轴（含端点）上的一个动点, 过P点斜率为k的直线l交椭圆与
A,B两点, 若|PA|2＋|PB|2的值仅依赖于k而与m无关, 求k的值．
如图, 平面
平面
, 
是以
为斜边的等腰直角三角形, 
分别为
, 
, 的中点, 
, 
．
(1) 设
是
的中点, 证明：
平面
；
(2) 证明：在
内存在一点
, 使
平面, 并求点到
, 
的距离．
已知数列
为等比数列, 其前
项和为
, 已知
, 且对于任意的
有, 
, 
成等差；求数列的通项公式；
如图, 已知单位圆上有四点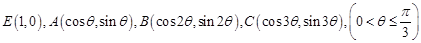
, 分别设
的面积为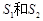
.
(1)用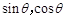
表示；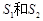
(2)求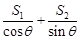
的最大值及取最大值时
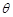的值.