如图, 平面 平面
平面 ,
,  是以
是以 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,  分别为
分别为 ,
,  ,
,  的中点,
的中点,  ,
,  .
.
(1) 设 是
是 的中点, 证明:
的中点, 证明: 平面
平面 ;
;
(2) 证明:在 内存在一点
内存在一点 , 使
, 使 平面
平面 , 并求点
, 并求点 到
到 ,
,  的距离.
的距离.
已知函数 ,
, .
.
(1)求 的单调增区间和最小值;
的单调增区间和最小值;
(2)若函数 与函数
与函数 在交点处存在公共切线,求实数
在交点处存在公共切线,求实数 的值;
的值;
(3)若 时,函数
时,函数 的图象恰好位于两条平行直线
的图象恰好位于两条平行直线
 ,
,
 之间,当
之间,当 与
与 间的距离最小时,求实数
间的距离最小时,求实数 的值.
的值.
如图, 为一直角三角形草坪,其中
为一直角三角形草坪,其中 ,
, 米,
米, 米,为了重建草坪,设计师准备了两套方案:
米,为了重建草坪,设计师准备了两套方案:
方案一:扩大为一个直角三角形,其中斜边 过点
过点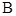 ,且与
,且与 平行,
平行, 过点
过点 ,
, 过点
过点 ;
;
方案二:扩大为一个等边三角形,其中 过点
过点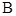 ,
, 过点
过点 ,
, 过点
过点 .
.
(1)求方案一中三角形 面积
面积 的最小值;
的最小值;
(2)求方案二中三角形 面积
面积 的最大值.
的最大值.
在等差数列 中,
中, ,其前
,其前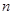 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,其前
,其前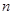 项和为
项和为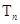 ,且
,且 ,
, .
.
(1)求数列 和数列
和数列 的通项;
的通项;
(2)问是否存在正整数 ,
,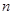 ,
, ,使得
,使得 成立?如果存在,请求出
成立?如果存在,请求出 ,
,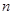 ,
, 的关系式;如果不存在,请说明理由.
的关系式;如果不存在,请说明理由.
已知椭圆
 (
( )的离心率为
)的离心率为 ,
,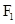 .
. 分别为椭圆
分别为椭圆 的左.右焦点,若椭圆
的左.右焦点,若椭圆 的焦距为
的焦距为 .
.
(1)求椭圆 的方程;
的方程;
(2)设 为椭圆上任意一点,以
为椭圆上任意一点,以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,当圆
,当圆 与椭圆的右准线
与椭圆的右准线 有公共点时,求
有公共点时,求 面积的最大值.
面积的最大值.
在正四面体 中,点
中,点 在
在 上,点
上,点 在
在 上,且
上,且 .
.
证明:(1)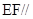 平面
平面 ;
;
(2)直线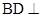 直线
直线 .
.