在等差数列 中,
中, ,其前
,其前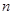 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,其前
,其前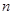 项和为
项和为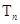 ,且
,且 ,
, .
.
(1)求数列 和数列
和数列 的通项;
的通项;
(2)问是否存在正整数 ,
,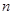 ,
, ,使得
,使得 成立?如果存在,请求出
成立?如果存在,请求出 ,
,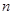 ,
, 的关系式;如果不存在,请说明理由.
的关系式;如果不存在,请说明理由.
(此题平行班做)(本小题满分12分)
某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:

(Ⅰ)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是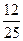 ,请完成上面的
,请完成上面的 列联表;
列联表;
 |
 |
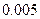 |
 |
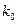 |
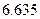 |
 |
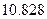 |
(Ⅱ)在(1)的条件下,试运用独立性检验的思想方法分析:在犯错误概率不超过0.1%的情况下判断学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
(本小题满分13分)
袋中有大小相同的三个球,编号分别为1、2和3,从袋中每次取出一个球,若取到的球的编号为偶数,则把该球编号加1(如:取到球的编号为2,改为3)后放回袋中继续取球;若取到球的编号为奇数,则取球停止,用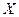 表示所有被取球的编号之和.
表示所有被取球的编号之和.
(Ⅰ)求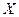 的概率分布;
的概率分布;
(Ⅱ)求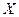 的数学期望与方差.
的数学期望与方差.
本小题满分12分)
在 的展开式中,第3项的系数与倒数第3项的系数之比为
的展开式中,第3项的系数与倒数第3项的系数之比为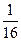 .
.
(Ⅰ)求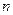 的值;
的值;
(Ⅱ)展开式的哪几项是有理项(回答项数即可);
(Ⅲ)求出展开式中系数最大的项.
(本小题满分12分)
若 ,则
,则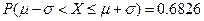 ,
,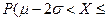
 ,
,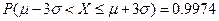 .在2010年黄冈中学理科实验班招生考试中,有5000人参加考试,考生的数学成绩服
.在2010年黄冈中学理科实验班招生考试中,有5000人参加考试,考生的数学成绩服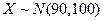 .
.
(Ⅰ)在5000名考生中,数学分数在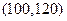 之间的考生约有多少人;
之间的考生约有多少人;
(Ⅱ)若对数学分数从高到低的前114名考生予以录取,问录取分数线为多少?
(本小题满分12分)命题p:关于x的不等式x2+2ax+4>0,对一切x∈R恒成立,q:函数 是增函数,若p或q为真,p且q为假,求实数a的取值范围.
是增函数,若p或q为真,p且q为假,求实数a的取值范围.