已知函数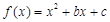 ,其中
,其中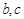 为常数.
为常数.
(Ⅰ)若函数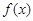 在区间
在区间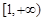 上单调,求
上单调,求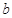 的取值范围;
的取值范围;
(Ⅱ)若对任意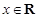 ,都有
,都有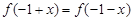 成立,且函数
成立,且函数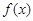 的图象经过点
的图象经过点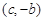 ,
,
求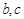 的值.
的值.
已知数列 满足
满足 (
( ).
).
(1)若数列 是等差数列,求它的首项和公差;
是等差数列,求它的首项和公差;
(2)证明:数列 不可能是等比数列;
不可能是等比数列;
(3)若 ,
, (
( ),试求实数
),试求实数 和
和 的值,使得数列
的值,使得数列 为等比数列;并求此时数列
为等比数列;并求此时数列 的通项公式.
的通项公式.
已知函数 和
和 的图像关于原点对称,且
的图像关于原点对称,且 .
.
(1)求函数 的解析式;
的解析式;
(2)解不等式 ;
;
(3)若函数 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,长轴长为
轴上,长轴长为 ,且点
,且点 在椭圆
在椭圆 上.
上.
(1)求椭圆 的方程;
的方程;
(2)设 是椭圆
是椭圆 长轴上的一个动点,过
长轴上的一个动点,过 作方向向量
作方向向量 的直线
的直线 交椭圆
交椭圆 于
于 、
、 两点,求证:
两点,求证: 为定值.
为定值.
设 ,函数
,函数 ,
, .
.
(1)求函数 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)若 ,求
,求 的值.
的值.