甲乙各自都有一个放有3个红球,2个白球,1个黄球共6个球的箱子.
(1)若甲在自己的箱子中任意取球,取后不放回. 每次只 取1个,直到取出红球为止,求甲取球的次数
取1个,直到取出红球为止,求甲取球的次数 的分布列和数学期望.
的分布列和数学期望.
(2)若甲乙各自从自己的箱子中任取一个球比颜色,规定同色时甲胜,异色时乙胜,这种游戏规则公平吗?请说明理由.
已知幂函数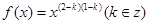 满足
满足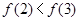 。
。
(1)求实数k的值,并写出相应的函数 的解析式;
的解析式;
(2)对于(1)中的函数 ,试判断是否存在正数m,使函数
,试判断是否存在正数m,使函数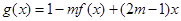 ,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。
(1)求实数a,b,并确定函数 的解析式;
的解析式;
(2)判断 在(-1,1)上的单调性,并用定义证明你的结论;
在(-1,1)上的单调性,并用定义证明你的结论;
(3)写出 的单调减区间,并判断
的单调减区间,并判断 有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
已知函数
(1)若函数 的图象经过P(3,4)点,求a的值;
的图象经过P(3,4)点,求a的值;
(2)比较 大小,并写出比较过程;
大小,并写出比较过程;
(3)若 ,求a的值.
,求a的值.
已知指数函数 ,当
,当 时,有
时,有 ,解关于x的不等式
,解关于x的不等式
已知函数 f(x)= 在[1,+∞)上为减函数,求实数a的取值范围.
在[1,+∞)上为减函数,求实数a的取值范围.