函数 ,其中
,其中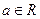
(1)若 在
在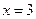 处取得极值,求
处取得极值,求 的值;
的值;
(2)若 在
在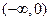 上为增函数,求
上为增函数,求 的取值范围
的取值范围
本小题满分12分)设直线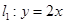 与直线
与直线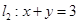 交于P点.
交于P点.
(Ⅰ)当直线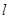 过P点,且与直线
过P点,且与直线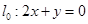 平行时,求直线
平行时,求直线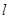 的方程.
的方程.
(Ⅱ)当直线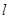 过P点,且原点O到直线
过P点,且原点O到直线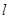 的距离为1时,求直线
的距离为1时,求直线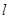 的方程.
的方程.
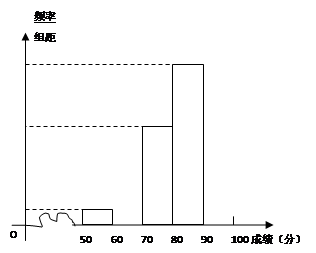
本小题满分12分)青少年“心理健康”问题越来越引起社会关注,某校对高二600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
(Ⅰ)填写答题卡频率分布表中的空格,并补全频率分布直方图;
(Ⅱ)试估计该年段成绩在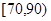 段的有多少人?
段的有多少人?
(Ⅲ)请你估算该年段分数的众数.
| 分 组 |
频 数 |
频 率 |
| [50,60) |
2 |
0.04 |
| [60,70) |
8 |
0.16 |
| [70,80) |
10 |
|
| [80,90) |
||
| [90,100] |
14 |
0.28 |
| 合 计 |
1.00 |
已知函数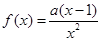 ,其中
,其中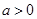 .
.
(1)求函数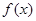 的单调区间;
的单调区间;
(2)若直线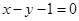 是曲线
是曲线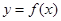 的切线,求实数
的切线,求实数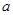 的值;
的值;
(3)设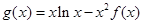 ,求
,求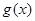 在区间
在区间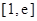 上的最小值.(其中
上的最小值.(其中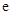 为自然对数的底数)
为自然对数的底数)
已知椭圆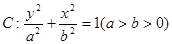 的两焦点与短轴的一个端点连结成等腰直角三角形,直线
的两焦点与短轴的一个端点连结成等腰直角三角形,直线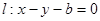 是抛物线
是抛物线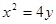 的一条切线。
的一条切线。
(1)求椭圆方程;
(2)直线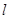 交椭圆
交椭圆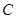 于A、B两点,若点P满足
于A、B两点,若点P满足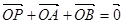 (O为坐标原点), 判断点P是否在椭圆
(O为坐标原点), 判断点P是否在椭圆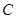 上,并说明理由。
上,并说明理由。
已知定义域为 的单调函数
的单调函数 是奇函数,当
是奇函数,当 时,
时, .
.
(1)求 的解析式;
的解析式;
(2)若对任意的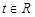 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.