如图,在四棱锥P ABCD中,侧面PAD⊥底面ABCD,侧棱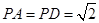 ,
, ,底面
,底面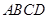 为直角梯形,其中BC∥AD, AB⊥AD,
为直角梯形,其中BC∥AD, AB⊥AD, 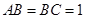 ,O为AD中点.
,O为AD中点.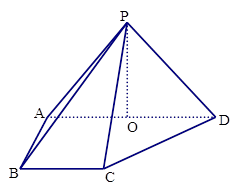
(1)求直线 与平面
与平面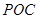 所成角的余弦值;
所成角的余弦值;
(2)求 点到平面
点到平面 的距离;
的距离;
(3)线段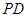 上是否存在一点
上是否存在一点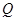 ,使得二面角
,使得二面角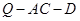 的余弦值为
的余弦值为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
选修4-4:坐标系与参数方程
己知抛物线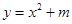 的顶点M到直线
的顶点M到直线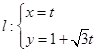 (t为参数)的距离为1
(t为参数)的距离为1
(1)求m;
(2)若直线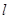 与抛物线相交于A,B两点,与y轴交于N点,求
与抛物线相交于A,B两点,与y轴交于N点,求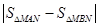 的值.
的值.
选修4-1:几何证明选讲
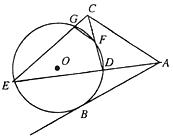
如图, 是
是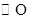 的一条切线,切点为
的一条切线,切点为 ,直线
,直线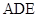 ,
,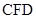 ,
,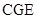 都是
都是 的割线,已知
的割线,已知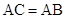 .
.
(1)求证: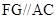 ;
;
(2)若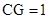 ,
,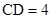 .求
.求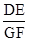 的值.
的值.
已知函数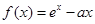 ,其中e为自然对数的底数,a为常数.
,其中e为自然对数的底数,a为常数.
(1)若对函数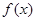 存在极小值,且极小值为0,求a的值;
存在极小值,且极小值为0,求a的值;
(2)若对任意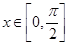 ,不等式
,不等式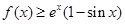 恒成立,求a的取值范围.
恒成立,求a的取值范围.
椭圆 过点
过点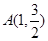 ,离心率为
,离心率为 ,左、右焦点分别为
,左、右焦点分别为 ,过
,过 的直线交椭圆于
的直线交椭圆于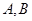 两点.
两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)当 的面积为
的面积为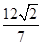 时,求直线的方程.
时,求直线的方程.
如图,在直三棱柱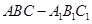 中,平面
中,平面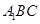
 侧面
侧面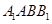 且
且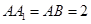 .
.
(Ⅰ)求证: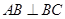 ;
;
(Ⅱ)若直线AC与平面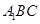 所成的角为
所成的角为 ,求锐二面角
,求锐二面角 的大小.
的大小.