选修4-1:几何证明选讲
如图, 是
是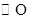 的一条切线,切点为
的一条切线,切点为 ,直线
,直线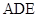 ,
,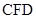 ,
,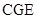 都是
都是 的割线,已知
的割线,已知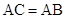 .
.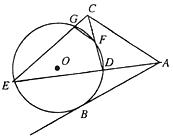
(1)求证: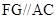 ;
;
(2)若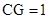 ,
,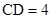 .求
.求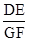 的值.
的值.
设函数f(x)对所有的实数x都满足f(x+2π)=f(x),求证:存在4个函数fi(x)(i=1,2,3,4)满足:(1)对i=1,2,3,4,fi(x)是偶函数,且对任意的实数x,有fi(x+π)=fi(x);(2)对任意的实数x,有f(x)=f1(x)+f2(x)cosx+f3(x)sinx+f4(x)sin2x。
已知过点(0,1)的直线l与曲线C: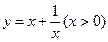 交于两个不同点M和N。求曲线C在点M、N处切线的交点轨迹。
交于两个不同点M和N。求曲线C在点M、N处切线的交点轨迹。
设集合P={1,2,3,4,5},对任意k∈P和正整数m,记f(m,k)=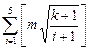 ,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。
,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。
如图,在7×8的长方形棋盘的每个小方格的中心点各放一个棋子。如果两个棋子所在的小方格共边或共顶点,那么称这两个棋子相连。现从这56个棋子中取出一些,使得棋盘上剩下的棋子,没有五个在一条直线(横、竖、斜方向)上依次相连。问最少取出多少个棋子才可能满足要求?并说明理由。
设 ,求证:当正整数n≥2时,an+1<an。
,求证:当正整数n≥2时,an+1<an。