两人相约在7点到8点在某地会面,先到者等候另一个人20分钟方可离去. 试求这两人能会面的概率?
如图,矩形花园ABCD,AB为4米,BC为6米,小鸟任意落下,则小鸟落在阴影区的概率是多少?
在空间直角坐标系中,已知A(3,0,1)和B(1,0,-3),试问
(1)在y轴上是否存在点M,满足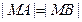 ?
?
(2)在y轴上是否存在点M,使△MAB为等边三角形?若存在,试求出点M坐标.
已知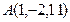 ,
,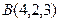 ,
, ,求证其为直角三角形.
,求证其为直角三角形.
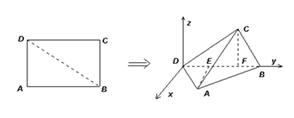
如图,已知矩形ABCD中,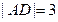 ,
,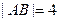 .将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.
.将矩形ABCD沿对角线BD折起,使得面BCD⊥面ABD.现以D为原点,DB作为y轴的正方向,建立如图空间直角坐标系,此时点A恰好在xDy坐标平面内.试求A,C两点的坐标.