为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别
进行抽样检查,测得身高频数分布表如下表1、表2. 表1:男生身高频数分布表
表1:男生身高频数分布表 表2:女生身高频数分布表
表2:女生身高频数分布表 (1)求该校男生的人数并完成下面频率分布直方图;
(1)求该校男生的人数并完成下面频率分布直方图;
(2)估计该校学生身高(单位:cm)在 的概率;
的概率;
(3)在男生样本中,从身高(单位:cm)在 的男生中任选3人,设
的男生中任选3人,设 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在 的人数,求
的人数,求 的分布列和数学期望.
的分布列和数学期望.
已知椭圆C的中心在原点,左焦点为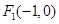 ,右准线方程为:
,右准线方程为: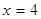 .
.
(1)求椭圆C的标准方程;
(2)若椭圆C上点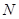 到定点
到定点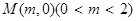 的距离的最小值为1,求
的距离的最小值为1,求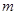 的值及点
的值及点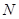 的坐标;
的坐标;
(3)分别过椭圆C的四个顶点作坐标轴的垂线,围成如图所示的矩形,A、B是所围成的矩形在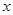 轴上方的两个顶点.若P、Q是椭圆C上两个动点,直线OP、OQ与椭圆的另一交点分别为
轴上方的两个顶点.若P、Q是椭圆C上两个动点,直线OP、OQ与椭圆的另一交点分别为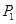 、
、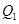 ,且直线OP、OQ的斜率之积等于直线OA、OB的斜率之积,试探求四边形
,且直线OP、OQ的斜率之积等于直线OA、OB的斜率之积,试探求四边形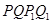 的面积是否为定值,并说明理由.
的面积是否为定值,并说明理由.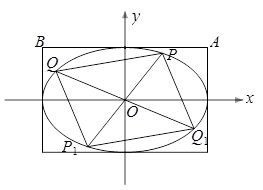
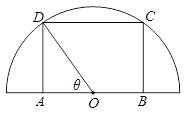
如图,在半径为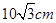 的半圆形(O为圆心)铁皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上,将所截得的矩形铁皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),记圆柱形罐子的体积为
的半圆形(O为圆心)铁皮上截取一块矩形材料ABCD,其中点A、B在直径上,点C、D在圆周上,将所截得的矩形铁皮ABCD卷成一个以AD为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),记圆柱形罐子的体积为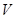
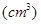 .
.
(1)按下列要求建立函数关系式:
①设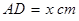 ,将
,将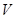 表示为
表示为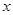 的函数;
的函数;
②设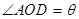 (
(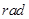 ),将
),将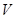 表示为
表示为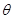 的函数;
的函数;
(2)请您选用(1)问中的一个函数关系,求圆柱形罐子的最大体积.
某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为 的样本,并将样本数据分成五组:
的样本,并将样本数据分成五组: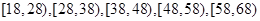 ,再将其按从左到右的顺序分别编号为第1组,第2组,
,再将其按从左到右的顺序分别编号为第1组,第2组,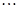 ,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.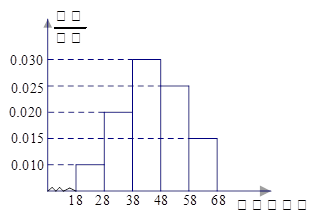
| 组号 |
分组 |
回答正确的人数 |
回答正确的人数占本组的比例 |
| 第1组 |
[18,28) |
5 |
0.5 |
| 第2组 |
[28,38) |
18 |
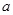 |
| 第3组 |
[38,48) |
27 |
0.9 |
| 第4组 |
[48,58) |
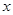 |
0.36 |
| 第5组 |
[58,68) |
3 |
0.2 |
(1)分别求出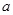 ,
,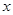 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
已知命题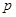 :实数
:实数 满足
满足 ;命题q:实数
;命题q:实数 满足
满足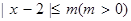 .
.
(1)当 时,若“
时,若“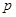 且
且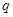 ”为真,求实数
”为真,求实数 的取值范围;
的取值范围;
(2)若“非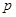 ”是“非
”是“非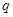 ”的必要不充分条件,求实数
”的必要不充分条件,求实数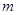 的取值范围.
的取值范围.
如图,斜三棱柱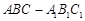 中,侧面
中,侧面 是菱形,
是菱形,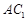 与
与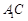 交于点
交于点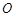 ,E是AB的中点.
,E是AB的中点.
求证:(1) 平面
平面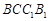 ;
;
(2)若 ,求证:
,求证: .
.