(满分12分) 
某商店按每件80元的价格,购进商品1000件(卖不出去的商品将成为废品);市场调研推知:当每件售价为100元时,恰好全部售完;当售价每提高1元时,销售量就减少5件;为获 得最大利润,商店决定提高售价
得最大利润,商店决定提高售价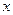 元,获得总利润
元,获得总利润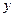 元.
元.
(1)请将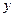 表示为
表示为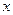 的函数;
的函数;
(2)当售价为多少时,总利润取最大值,并求出此时的利润.
(本小题满分12分)
(方案一)已知: ,
,  与
与 的夹角为
的夹角为 ,
, (
( )当m为何值时,
)当m为何值时, 与
与 垂直?
垂直?
(本小题满分10分)
求不等式 的解集.
的解集.
已知数列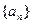 中
中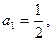 点
点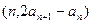
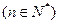 在直线
在直线 上.
上.
(1)计算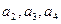 的值;
的值;
(2)令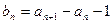 ,求证
,求证 是等比数列;
是等比数列;

(3)设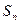 、
、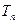 分别为数列
分别为数列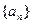 、
、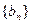 的前
的前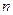 项和,是否存在实数
项和,是否存在实数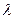 ,使得数列
,使得数列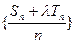 为等差数列?若存在,试求出
为等差数列?若存在,试求出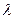 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:米),修建此矩形场地围墙的总费用为y (单位:元).
(1)将y表示为x的函数;
(2)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.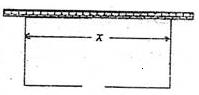
(本题满分12分)
已知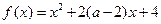 ,
,
(1)如果对一切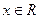 ,
,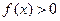 恒成立,求实数
恒成立,求实数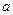 的取值范围;
的取值范围;
(2)如果对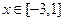 ,
,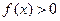 恒成立,求实数
恒成立,求实数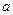 的取值范围.
的取值范围.