已知数列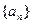 中
中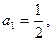 点
点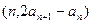
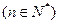 在直线
在直线 上.
上.
(1)计算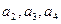 的值;
的值;
(2)令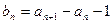 ,求证
,求证 是等比数列;
是等比数列;

(3)设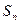 、
、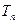 分别为数列
分别为数列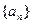 、
、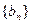 的前
的前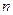 项和,是否存在实数
项和,是否存在实数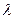 ,使得数列
,使得数列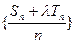 为等差数列?若存在,试求出
为等差数列?若存在,试求出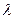 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
设函数

(1)若 ,
,
①求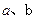 的值;
的值;
②在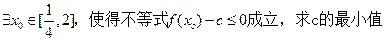 ;
;
(2)当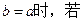
 上是单调函数,求
上是单调函数,求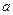 的取值范围。
的取值范围。
(参考数据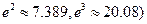
已知点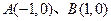 ,直线
,直线 相交于点
相交于点 ,且它们的斜率之积为
,且它们的斜率之积为 ,
,
(1)求动点 的轨迹
的轨迹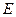 的方程;
的方程;
(2)若过点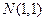 的直线
的直线 与曲线
与曲线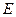 交于
交于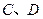 两点,且
两点,且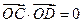 ,求直线
,求直线 的方程.
的方程.
已知双曲线 的中心在原点,焦点在坐标轴上,离心率
的中心在原点,焦点在坐标轴上,离心率 ,且双曲线过点
,且双曲线过点 ,求双曲线
,求双曲线 的方程.
的方程.
已知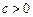 且
且 ,设命题
,设命题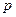 :函数
:函数 在R上单调递减,命题
在R上单调递减,命题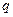 :不等式
:不等式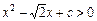 的解集为R,如果命题“
的解集为R,如果命题“ ”为真命题,“
”为真命题,“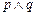 ”为假命题,求实数
”为假命题,求实数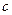 的取值范围
的取值范围
某餐厅供应客饭,每位顾客可以在餐厅提供的菜肴中任选2荤2素共4种不同的品种,现在餐厅准备了 5种不同的荤菜,若要保证每位顾客有200种以上的不同选择,则餐厅至少还需准备不同的素菜品种多少种?