（本小题满分16分）
某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中，发现其在
40分钟的一节课中，注意力指数p与听课时间t（单位：分钟）之间的关系满足如图
所示的曲线．当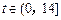
时
，曲线是二次函数图象的一部分，当
时，曲线
是函数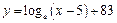
(
，
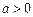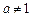)图象的一部分．根据专家研究，当注意力指数p大于80时学习效果最佳．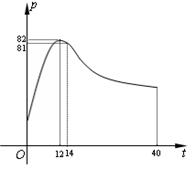
（1）试求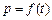
的函数关系式；
（2）教师在什么时段内安排核
心内容，能使得学生学习效果最佳？请说明理由．
设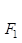
,
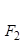分别是椭圆E：
+
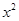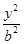=1（0﹤b﹤1）的左、右焦点，过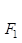的直线与E相交于A、B两点，且
，
，
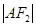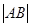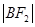成等差数列。
（1）求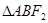
的周长
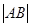（2）求的长
（3）若直线的斜率为1，求b的值。
（本小题１4分）请你设计一个包装盒，如图所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得ABCD四个点重合于图中的点P，正好形成一个正四棱柱（底面是正方形的直棱柱）形状的包装盒，E、F在AB上是被切去的等腰直角三角形HEF斜边的两个端点，设AE=FB=xcm.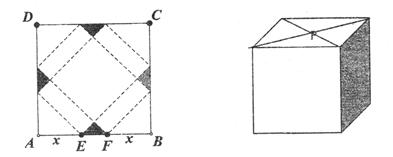
（１）请用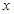
分别表示｜GE｜、｜EH｜的长
（2）若广告商要求包装盒侧面积S（cm2）最大，试问x应取何值？
|
（3）若广告商要求包装盒容积V（cm3）最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值.
（本小题１4分）设函数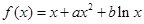
，曲线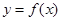
过P（1,0），且在P点处的切斜线率为2．
（I）求a，b的值；
（II）证明：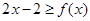
．
（本小题１4分）如图，四棱锥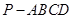
中，底面ABCD为平行四边形，
，
，
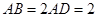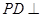底面ABCD．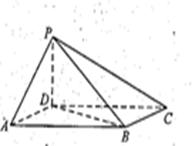
（1）求|DB|的长
（2）证明：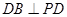
；
（3）若PD=AD，求二面角D-PA-B的余弦值．
（本小题１２分）已知函数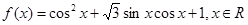
．
（1）求函数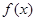
的最小正周期及单调增区间；
（2）求函数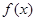在
上的最大值和最小值，并求函数取得最大值和最小值时的自变量
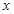的值．