已知点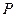 为圆
为圆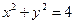 上的动点,且
上的动点,且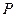 不在
不在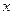 轴上,
轴上,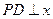 轴,垂足为
轴,垂足为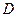 ,线段
,线段 中点
中点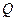 的轨迹为曲线
的轨迹为曲线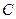 ,过定点
,过定点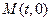
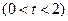 任作一条与
任作一条与 轴不垂直的直线
轴不垂直的直线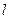 ,它与曲线
,它与曲线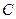 交于
交于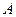 、
、 两点。
两点。
(1)求曲线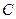 的方程;
的方程;
(2)试证明:在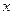 轴上存在定点
轴上存在定点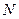 ,使得
,使得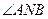 总能被
总能被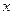 轴平分。
轴平分。
证明:已知 ,则
,则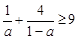
设 为数列
为数列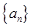 的前
的前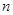 项和,对任意的
项和,对任意的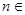 N,都有
N,都有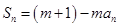
 为常数,且
为常数,且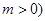 .
.
(1)求证:数列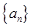 是等比数列;
是等比数列;
(2)设数列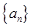 的公比
的公比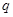 与
与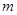 函数关系为
函数关系为 ,数列
,数列 满足
满足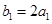 ,点
,点 落在
落在  上,
上, ,
,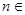 N,求数列
N,求数列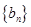 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列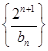 的前
的前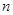 项和
项和 ,使
,使
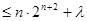 恒成立时,求
恒成立时,求 的最小值.[
的最小值.[
某房地产开发商投资81万元建一座写字楼,第一年需维护费用为1万元,以后每年增加2万元,若把写字楼出租,每年收入租金30万元.
(1)开发商最早在第几年获取纯利润?
(2)若干年后开发商为了投资其它项目,有两种处理方案:①纯利润最大时,以10万元出售该楼;②年平均利润最大时以46万元出售该楼.问哪种方案更优?并说明理由?
若不等式组 (其中
(其中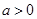 )表示的平面区域的面积是9.
)表示的平面区域的面积是9.
(1)求 的值;(2)求
的值;(2)求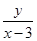 的最小值,及此时
的最小值,及此时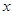 与
与 的值.
的值.
已知 、
、 、
、 分别是
分别是 的三个内角
的三个内角 、
、 、
、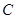 所对的边
所对的边
(1)若 面积
面积 求
求 、
、 的值;
的值;
(2)若 ,试判断
,试判断 的形状.
的形状.