(本小题满分14分)
设两个非零向量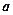 与
与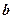 不共线,
不共线,
(1)若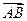 =
=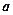 +
+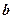 ,
,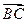 =2
=2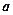 +8
+8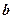 ,
,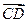 =3(
=3(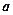 -
-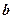 ),求证:
),求证: 三点共线;
三点共线;
(2)试确定实数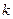 ,使
,使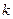
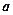 +
+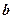 和
和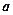 +
+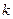
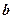 共线.
共线.
如图是从一副扑克牌中取出的两组牌,分别是黑桃2、3、4和方块2、3、4,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌的牌面数字之和等于5的概率是多少?请你用列表或画树状图加以分析说明.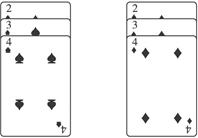
将一个骰子连续掷三次,出现“一次1点,一次2点,一次3点”的概率是多少?
盒中有大小形状相同的5个白球和2个黑球,求下列事件的概率:
(1)任取一球,得到白球。
(2)任取三球,恰有2个白球。
(3)任取三球(分3次,每次放回后再取),恰有3个白球。
已知有一对夫妇有且只有两个孩子,某天你打电话到他们家,是一个孩子接的电话,这个孩子是女孩,请问,另一个孩子也是女孩的概率是多少?
已知一对夫妇有且只有两个孩子,其中一个是女孩,请问,另一个孩子也是女孩的概率是多少?