(本小题满分16分)
已知函数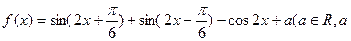 为常数).
为常数).
(1)求函数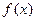 的最小正周期; (2)求函数
的最小正周期; (2)求函数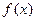 的单调递增区间;
的单调递增区间;
(3) 若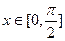 时,
时,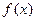 的最小值为
的最小值为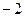 ,求
,求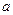 的值.
的值.
右图为一简单组合体,其底面ABCD为正方形, 平面
平面 ,
, ,且
,且 ="2" .
="2" .
(1)求四棱锥B-CEPD的体积;
(2)求证: 平面
平面 .
. 
已知复数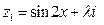 ,
,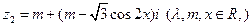 ,且
,且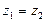 .
.
(1)若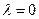 且
且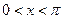 ,求
,求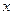 的值;
的值;
(2)设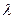 =
=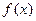 ,求
,求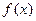 的最小正周期和单调减区间.
的最小正周期和单调减区间.
(本小题满分14分)
下表给出的是由n×n(n≥3,n∈N*)个正数排成的n行n列数表,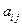 表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为
表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为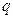 ,若已知
,若已知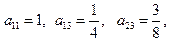
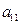 |
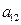 |
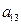 |
… |
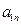 |
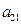 |
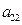 |
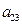 |
… |
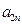 |
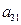 |
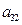 |
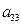 |
… |
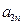 |
| … |
… |
… |
… |
… |
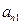 |
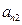 |
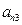 |
… |
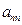 |
(1)求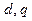 的值;
的值;
(2)求用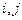 表示
表示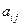 的代数式;
的代数式;
(3)设表中对角线上的数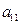 ,
,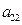 ,
,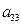 ,……,
,……,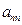 组成一列数列,设Tn=
组成一列数列,设Tn=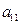 +
+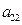 +
+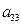 +……+
+……+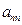 求使不等式
求使不等式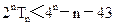 成立的最小正整数n.
成立的最小正整数n.
(本小题满分14分)已知函数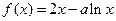 (
(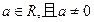 )
)
(1) 判断函数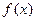 的单调性;
的单调性;
(2) 是否存在实数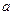 使得函数
使得函数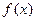 在区间
在区间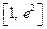 上有最小值恰为
上有最小值恰为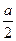 ? 若存在,求出
? 若存在,求出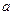 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分14分)已知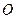 为坐标原点,点F、T、M、P分别满足
为坐标原点,点F、T、M、P分别满足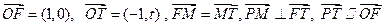 .
.
(1) 当t变化时,求点P的轨迹方程;
(2) 若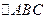 的顶点在点P的轨迹上,且点A的纵坐标
的顶点在点P的轨迹上,且点A的纵坐标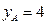 ,
,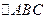 的重心恰好为点F,
的重心恰好为点F,
求直线BC的方程.