(本小题满分14分)
下表给出的是由n×n(n≥3,n∈N*)个正数排成的n行n列数表,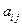 表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为
表示第i行第j列的数,表中第一列的数从上到下依次成等差数列,其公差为d ,表中各行中每一行的数从左到右依次都成等比数列,且所有公比相等,公比为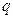 ,若已知
,若已知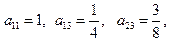
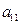 |
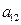 |
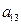 |
… |
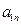 |
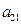 |
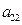 |
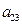 |
… |
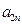 |
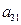 |
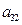 |
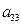 |
… |
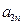 |
| … |
… |
… |
… |
… |
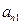 |
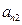 |
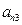 |
… |
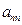 |
(1)求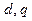 的值;
的值;
(2)求用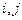 表示
表示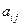 的代数式;
的代数式;
(3)设表中对角线上的数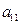 ,
,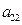 ,
,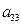 ,……,
,……,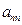 组成一列数列,设Tn=
组成一列数列,设Tn=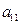 +
+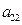 +
+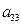 +……+
+……+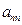 求使不等式
求使不等式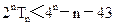 成立的最小正整数n.
成立的最小正整数n.
本题满分14分)
设函数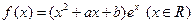 .
.
(1)若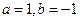 ,求函数
,求函数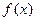 的极值;
的极值;
(2)若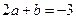 ,试确定
,试确定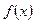 的单调性;
的单调性;
(3)记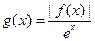 ,且
,且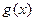 在
在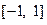 上的最大值为M,证明:
上的最大值为M,证明: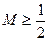 .
.
在数列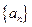 中,已知
中,已知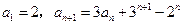
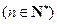 .
.
(1)求数列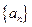 的通项公式;
的通项公式;
(2)求数列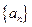 的前
的前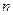 项和
项和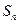 .
.
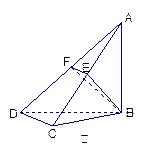
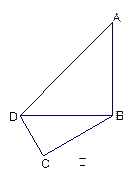
如图甲,在平面四边形ABCD中,已知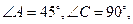
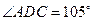 ,
,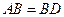 ,现将四边形ABCD沿BD折起,
,现将四边形ABCD沿BD折起,
使平面ABD 平面BDC(如图乙),设点E、F分别为棱
平面BDC(如图乙),设点E、F分别为棱
AC、AD的中点.
(1)求证:DC 平面ABC;
平面ABC;
(2)求BF与平面ABC所成角的正弦;
(3)求二面角B-EF-A的余弦.
已知椭圆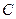 :
: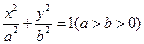 的长轴长是短轴长的
的长轴长是短轴长的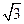 倍,
倍,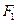 ,
,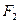 是它的左,右焦点.
是它的左,右焦点.
(1)若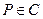 ,且
,且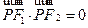 ,
,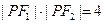 ,求
,求 、
、 的坐标;
的坐标;
(2)在(1)的条件下,过动点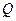 作以
作以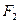 为圆心、以1为半径的圆的切线
为圆心、以1为半径的圆的切线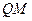 (
(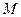 是切点),且使
是切点),且使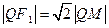 ,求动点
,求动点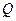 的轨迹方程.
的轨迹方程.
为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别
进行抽样检查,测得身高频数分布表如下表1、表2. 表1:男生身高频数分布表
表1:男生身高频数分布表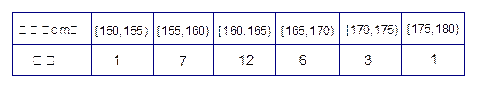 表2:女生身高频数分布表
表2:女生身高频数分布表
(1)求该校男生的人数并完成下面频率分布直方图;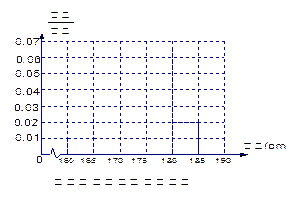
(2)估计该校学生身高(单位:cm)在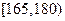 的概率;
的概率;
(3)在男生样本中,从身高(单位:cm)在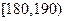 的男生中任选3人,设
的男生中任选3人,设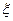 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在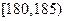 的人数,求
的人数,求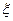 的分布列和数学期望.
的分布列和数学期望.