为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别
进行抽样检查,测得身高频数分布表如下表1、表2. 表1:男生身高频数分布表
表1:男生身高频数分布表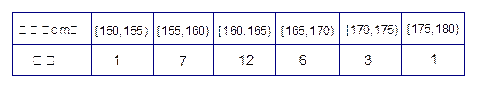 表2:女生身高频数分布表
表2:女生身高频数分布表
(1)求该校男生的人数并完成下面频率分布直方图;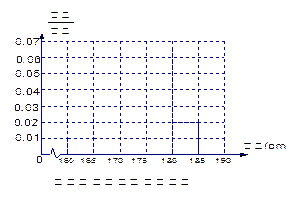
(2)估计该校学生身高(单位:cm)在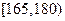 的概率;
的概率;
(3)在男生样本中,从身高(单位:cm)在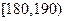 的男生中任选3人,设
的男生中任选3人,设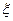 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在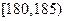 的人数,求
的人数,求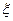 的分布列和数学期望.
的分布列和数学期望.
已知:函数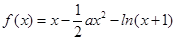 ,其中
,其中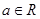 .
.
(Ⅰ)若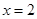 是
是 的极值点,求
的极值点,求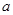 的值;
的值;
(Ⅱ)求 的单调区间;
的单调区间;
(Ⅲ)若 在
在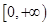 上的最大值是
上的最大值是 ,求
,求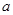 的取值范围.
的取值范围.
某商场销售某种商品的经验表明,该商品每日的销售量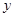 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:
(单位:
元/千克)满足关系式 .其中
.其中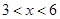 ,
,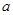 为常数.已知销售价格为
为常数.已知销售价格为 元/千克时,每
元/千克时,每
日可售出该商品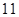 千克.
千克.
(Ⅰ)求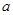 的值;
的值;
(Ⅱ)若该商品的成本为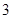 元/千克,试确定销售价格
元/千克,试确定销售价格 的值,使商场每日销售该商品所获得的利润最大.
的值,使商场每日销售该商品所获得的利润最大.
甲、乙两支球队进行总决赛,比赛采用七场四胜制,即若有一队先胜四场,则此队为总冠军,比赛就此结束.因两队实力相当,每场比赛两队获胜的可能性均为二分之一.据以往资料统计,第一场比赛可获得门票收入 万元,以后每场比赛门票收入比上一场增加
万元,以后每场比赛门票收入比上一场增加 万元.
万元.
(Ⅰ)求总决赛中获得门票总收入恰好为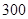 万元的概率;
万元的概率;
(Ⅱ)设总决赛中获得的门票总收入为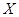 ,求
,求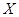 的分布列.
的分布列.
当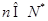 时,
时, ,
,
(Ⅰ)求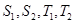 ;
;
(Ⅱ)猜想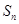 与
与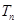 的关系,并用数学归纳法证明.
的关系,并用数学归纳法证明.
已知 ,且
,且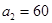 .
.
(Ⅰ)求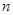 的值;
的值;
(Ⅱ)求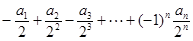 的值.
的值.