(本小题满分16分)
给定两个长度为1的平面向量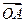 和
和 ,它们的夹角为
,它们的夹角为 .
.
(1)求|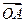 +
+ |;
|;
(2)如图(1)所示,点 在以
在以 为圆心的圆弧⌒AB上运动.若
为圆心的圆弧⌒AB上运动.若
其中 ,求
,求 的最大值?
的最大值?
(3)若点 、点
、点 在以
在以 为圆心,1为半径的圆上,且
为圆心,1为半径的圆上,且 ,问
,问 与
与 的夹角
的夹角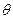 取何值时,
取何值时, 的值最大?并求出这个最大值.
的值最大?并求出这个最大值.
图(1) 图(2)
设集合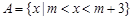 ,
, ,分别求满足下列条件的实数
,分别求满足下列条件的实数 的取值或取值范围:
的取值或取值范围:
(1)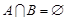 ;
;
(2)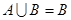 .
.
(1)求值: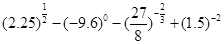 ;
;
(2)解不等式: .
.
(本小题满分14分)如图,椭圆 :
: 的左焦点为
的左焦点为 ,右焦点为
,右焦点为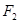 ,离心率
,离心率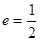 .过
.过 的直线交椭圆于
的直线交椭圆于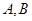 两点,且△
两点,且△ 的周长为
的周长为 .
.
(Ⅰ)求椭圆 的方程.
的方程.
(Ⅱ)设动直线 :
: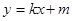 与椭圆
与椭圆 有且只有一个公共点
有且只有一个公共点 ,且与直线
,且与直线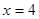 相交于点
相交于点 .试探究:在坐标平面内是否存在定点
.试探究:在坐标平面内是否存在定点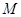 ,使得以
,使得以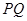 为直径的圆恒过点
为直径的圆恒过点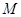 ?若存在,求出点
?若存在,求出点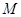 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(本小题13分)如图,棱锥 的底面
的底面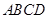 是矩形,
是矩形,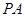 ⊥平面
⊥平面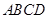 ,
,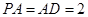 ,
,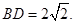

(1)求证: ⊥平面
⊥平面 ;
;
(2)求二面角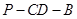 的大小;
的大小;
(3)求点 到平面
到平面 的距离.
的距离.
某商场举行抽奖活动,从装有编号0,1,2,3四个球的抽奖箱中,每次取出后放回,连续取两次,取出的两个小球号码相加之和等于5中一等奖,等于4中二等奖,等于3中三等奖。
(1)求中二等奖的概率;
(2)求未中奖的概率。