(本小题满分13分)已知 是腰长为2的等腰直角三角形(如图1),
是腰长为2的等腰直角三角形(如图1), ,在边
,在边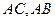 上分别取点
上分别取点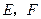 ,使得
,使得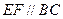 ,把
,把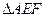 沿直线
沿直线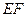 折起,使
折起,使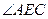 =90°,得四棱锥
=90°,得四棱锥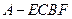 (如图2).在四棱锥
(如图2).在四棱锥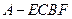 中,
中,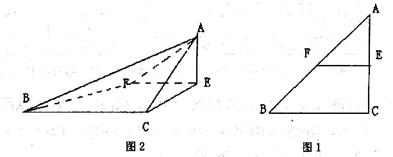
 (I)求证:CE⊥AF;
(I)求证:CE⊥AF;  (II)当
(II)当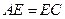 时,试在
时,试在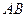 上确定一点G,使得
上确定一点G,使得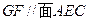 ,并证明你的结论.
,并证明你的结论.




试说明矩形的四个顶点在以对角线的交点为圆心的同一个圆上.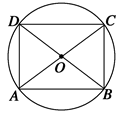
(拓展深化)如图①所示,△ABC内接于⊙O,AB=AC,D是BC边上的一点,E是直线AD和△ABC外接圆的交点.
(1)求证:AB2=AD·AE;
(2)如图②所示,当D为BC延长线上的一点时,第(1)题的结论成立吗?若成立,请证明;若不成立,请说明理由.
如图所示,AB是⊙O的直径,弦AC=3 cm,BC=4 cm,CD⊥AB,垂足为D,求AD、BD和CD的长.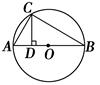
定义在R上的函数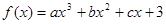 同时满足以下条件:
同时满足以下条件:
① 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数;
② 是偶函数;
是偶函数;
③ 在x=0处的切线与直线y=x+2垂直.
在x=0处的切线与直线y=x+2垂直.
(1)求函数 的解析式;
的解析式;
(2)设g(x)=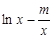 ,若存在实数x∈[1,e],使g(x)<
,若存在实数x∈[1,e],使g(x)< ,求实数m的取值范围。
,求实数m的取值范围。
已知动点P与平面上两定点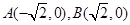 连线的斜率的积为定值
连线的斜率的积为定值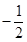 .
.
(1)试求动点P的轨迹方程C.
(2)设直线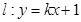 与曲线C交于M、N两点,当|MN|=
与曲线C交于M、N两点,当|MN|= 时,求直线l的方程.
时,求直线l的方程.