如图,在梯形ABCD中,AD∥BC,AB="DC" ,过点D作DE∥AB 交BC于点E.
(1) 请你判断四边形ABED的形状,并说明理由;
(2) 当△DEC为等边三角形时,
① 求∠B的度数;
② 若AD=4,DC=3,求等腰梯形ABCD的周长.
问题背景:已知在△ABC中,AB边上的动点D由A向B运动(与A,B不重合),点E与点D同时出发,由点C沿BC的延长线方向运动(E不与C重合),连结DE交AC于点F,点H是线段AF上一点
(1)初步尝试:如图1,若△ABC是等边三角形,DH⊥AC,且点D,E的运动速度相等,求证:HF=AH+CF
小王同学发现可以由以下两种思路解决此问题:
思路一:过点D作DG∥BC,交AC于点G,先证GH=AH,再证GF=CF,从而证得结论成立.
思路二:过点E作EM⊥AC,交AC的延长线于点M,先证CM=AH,再证HF=MF,从而证得结论成立.
请你任选一种思路,完整地书写本小题的证明过程(如用两种方法作答,则以第一种方法评分)
(2)类比探究:如图2,若在△ABC中,∠ABC=90°,∠ADH=∠BAC=30°,且点D,E的运动速度之比是 :1,求
:1,求 的值.
的值.
(3)延伸拓展:如图3,若在△ABC中,AB=AC,∠ADH=∠BAC=36°,记 =m,且点D、E的运动速度相等,试用含m的代数式表示
=m,且点D、E的运动速度相等,试用含m的代数式表示 (直接写出结果,不必写解答过程).
(直接写出结果,不必写解答过程).
某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产的零件个数和规定的天数.
(2)为了提前完成生产任务,工厂在安排原有工人按原计划正常生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%,按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人人数.
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
某校被调查学生选择社团意向统计表
| 选择意向 |
文学鉴赏 |
科学实验 |
音乐舞蹈 |
手工编织 |
其他 |
| 所占百分比 |
a |
35% |
b |
10% |
c |
根据统计图表中的信息,解答下列问题:
(1)求本次调查的学生总人数及a,b,c的值.
(2)将条形统计图补充完整(温馨提示:请画在答题卷相对应的图上).
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数.
如图,已知BC是⊙O的直径,AC切⊙O于点C,AB交⊙O于点D,E为AC的中点,连结DE.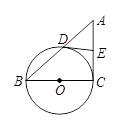
(1)若AD=DB,OC=5,求切线AC的长.
(2)求证:ED是⊙O的切线.
已知y是x的一次函数,当x=3时,y=1;当x=−2时,y=−4,求这个一次函数的解析式.