各项均为正数的数列 的前
的前 项和为
项和为 ,满足
,满足
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,
,
数列 满足
满足 ,数列
,数列 的前
的前
 项和为
项和为 ,求
,求 ;
;
(3)若数列 ,甲同学利用第(2)问中的
,甲同学利用第(2)问中的 ,试图确定
,试图确定 的值是否可以等于2011?为此,他设计了一个程序
的值是否可以等于2011?为此,他设计了一个程序 (如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。
(如图),但乙同学认为这个程序如果被执行会是一个“死循环”(即程序会永远循环下去,而无法结束),你是否同意乙同学的观点?请说明理由。
如图,已知在侧棱垂直于底面三棱柱 中,
中,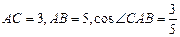 ,
,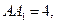 点
点 是
是 的中点。
的中点。
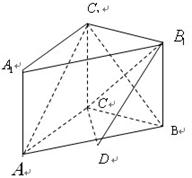
(1)求证: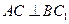
(2)求证:
(3)求三棱锥  的体积。
的体积。
求过点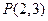 ,且在两坐标轴上的截距相等的直线方程。
,且在两坐标轴上的截距相等的直线方程。
三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18. (本小题满分14分) A、B是单位圆O上的动点,且A、B分别在第一、二象限,C是圆O与轴正半轴的交点,
(本小题满分14分) A、B是单位圆O上的动点,且A、B分别在第一、二象限,C是圆O与轴正半轴的交点,  为等腰直角三角形。记
为等腰直角三角形。记 (1)若A点的坐标为
(1)若A点的坐标为 ,求
,求  的值 (2)求
的值 (2)求 的取值范围。
的取值范围。
 |
已知函数 ,
,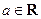 .
.
(Ⅰ)当a=2时,求函数 的单调区间及极值;
的单调区间及极值;
(Ⅱ)设函数 在区间
在区间 内是减函数,求
内是减函数,求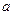 的取值范围.
的取值范围.
如图,在 四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=AD.
四棱锥P-ABCD中,底面ABCD是边长为a的正方形,E、F分别为PC、BD的中点,侧面PAD⊥底面ABCD,且PA=PD=AD.
(1)求证:EF∥平面PAD;
(2)求证:直线CD⊥平面PAD
(3)求证:面PAD⊥平面PCD.