设定义在R上的函数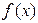 满足:①
满足:① 对任意的实数
对任意的实数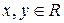 ,有
,有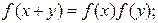 ②当
②当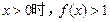 .
.
数列 满足
满足 .
.
(1)求证: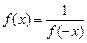 ,并判断函数
,并判断函数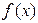 的单调性;
的单调性;
(2)令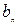 是最接近
是最接近 的正整数,即
的正整数,即 ,
,
设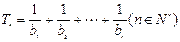 ,求
,求 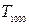 ;
;
(本小题满分13分)
已知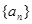 是单调递增的等差数列,首项
是单调递增的等差数列,首项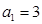 ,前
,前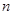 项和为
项和为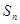 ,数列
,数列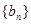 是等比数列,首项
是等比数列,首项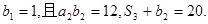 (Ⅰ)求
(Ⅰ)求 的通项公式。
的通项公式。
(Ⅱ)令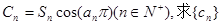 的前n项和
的前n项和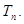
(本小题满分12分)已知椭圆的焦点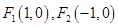 ,过
,过 作垂直于
作垂直于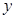 轴的直线被椭圆所截线段长为
轴的直线被椭圆所截线段长为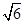 ,过
,过 作直线l与椭圆交于A、B两点.(I)求椭圆的标准方程;(Ⅱ)是否存在实数
作直线l与椭圆交于A、B两点.(I)求椭圆的标准方程;(Ⅱ)是否存在实数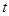 使
使 ,若存在,求
,若存在,求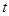 的值和直线
的值和直线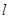 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(本小题满分12分).
如图是某直三棱柱被削去上底后所得几何体的直观图、左视图、俯视图,在直观图中,M是
BD的中点,左视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示。
(Ⅰ)求该几何体的体积;(Ⅱ)求证:EM∥平面ABC;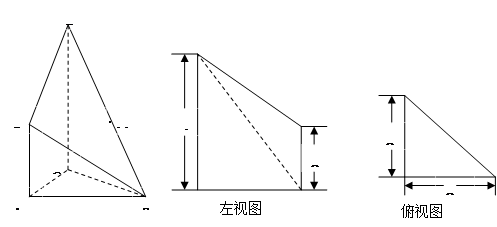
(本小题满分12分)
某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用
品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
| X |
1 |
2 |
3 |
4 |
5 |
| 频率 |
a |
0.2 |
0.4 |
b |
c |
(I)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,
求a,b,c的值;
(Ⅱ)在(I)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件
日用品记为y1,y2,现从x1,x2,x3,y1,y2这5件日用品中任取两件(假定每件日用品被取出
的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率
(本小题满分12分)
在 中,
中, .
.
(I)求角 的大小;
的大小;
(II)若 ,
,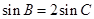 ,求
,求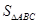 .
.