某学校要刻录一批电脑光盘,若到电脑公司刻录,每张需要8元;若学校自己刻,除租用刻录机需要120元外,每张还需要成本4元。
(1)刻录多少张光盘时,到电脑公司刻录与学校自己刻录所需费用一样?
(2)刻录多少张光盘时,到电脑公司刻录较合算?
(3)刻录多少张光盘时,学校自己刻录较合算?
(1)计算: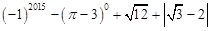 ;(2)化简:
;(2)化简: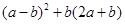 .
.
在平面直角坐标系中,抛物线C :y=
:y= x
x +4x+4
+4x+4 (0<
(0< <2),
<2),

(1)当C 与x轴有唯一交点时,求C
与x轴有唯一交点时,求C 的解析式;
的解析式;
(2)若 =1,将抛物线C
=1,将抛物线C 先向右平移2个单位,再向下平移1个单位得抛物线C
先向右平移2个单位,再向下平移1个单位得抛物线C ,抛物线C
,抛物线C 与x轴相交于M、N两点(M点在N点的左边),直线y=kx(k>0)与抛物线C
与x轴相交于M、N两点(M点在N点的左边),直线y=kx(k>0)与抛物线C 相交于P、Q(P在第三象限)且△NOQ的面积是△MOP的面积的4倍,求k的值;
相交于P、Q(P在第三象限)且△NOQ的面积是△MOP的面积的4倍,求k的值;
(3)若A(1,y ),B(0,y
),B(0,y ),C(-1,y
),C(-1,y )三点均在C
)三点均在C 上,连BC,作AE∥BC交抛物线C
上,连BC,作AE∥BC交抛物线C 于E,求证:当
于E,求证:当 值变化时,E点在一条直线上.
值变化时,E点在一条直线上.
(本题10分)如图1,梯形ABCD中AB∥CD,且AB=2CD,点P为BD的中点,直线AP交BC于E,交DC的延长线于F.

(1)求证:DC=CF;
(2)求 的值;
的值;
(3)如图2,连接DE,若AD⊥ED,求证: BAE=
BAE= DBE.
DBE.
某校学生参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如表所示:
| 销售单价x(单位:元/个) |
10 |
12 |
14 |
16 |
| 销售量y(单位:个) |
300 |
240 |
180 |
120 |
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;
(3)在(2)的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
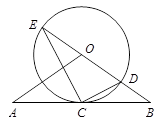
如图,直线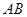 经过
经过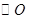 上的点
上的点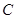 ,并且
,并且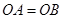 ,
,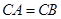 ,
,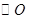 交直线
交直线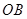 于
于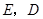 ,连接
,连接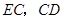 .
. [
[
(1)求证:直线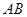 是
是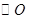 的切线;
的切线;
(2)若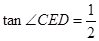 ,
,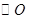 的半径为3,求
的半径为3,求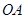 的长.
的长.