某校学生参加社会公益活动，准备购进一批许愿瓶进行销售，并将所得利润捐给慈善机构．根据市场调查，这种许愿瓶一段时间内的销售量y（个）与销售单价x（元/个）之间的对应关系如表所示：
| 销售单价x（单位：元/个） |
10 |
12 |
14 |
16 |
| 销售量y(单位：个) |
300 |
240 |
180 |
120 |
（1）试判断y与x之间的函数关系，并求出函数关系式；
（2）若许愿瓶的进价为6元/个，按照上述市场调查的销售规律，求销售利润w（元）与销售单价x（元/个）之间的函数关系式；
（3）在（2）的条件下，若许愿瓶的进货成本不超过900元，要想获得最大利润，试确定这种许愿瓶的销售单价，并求出此时的最大利润．
如图，已知∠MON两边分别为OM、ON，sin∠O=
且OA=5，点D为线段OA上的动点（不与O重合），以A为圆心、AD为半径作⊙A，设OD=x．
（1）若⊙A交∠O 的边OM于B、C两点，BC=y，求y关于x的函数解析式，并写出函数的定义域；
（2）将⊙A沿直线OM翻折后得到⊙A′．
①若⊙A′与直线OA相切，求x的值；
②若⊙A′与以D为圆心、DO为半径的⊙D相切，求x的值．
如图，直线y=4x+4与x轴、y轴相交于B、C两点，抛物线y=ax2-2ax+c（a≠0）过点B、C，且与x轴另一个交点为A，以OC、OA为边作矩形OADC，CD交抛物线于点G．
（1）求抛物线的解析式以及点A的坐标；
（2）已知直线x=m交OA于点E，交CD于点F，交AC于点M，交抛物线（CD上方部分）于点P，请用含m的代数式表示PM的长；
（3）在（2）的条件下，联结PC，若△PCF和△AEM相似，求m的值．
已知：如图，在梯形ABCD中，AD∥BC，∠ABC=90°，BC=2AD，点E是BC的中点、F是CD上的点，联结AE、EF、AC．
（1）求证：AO•OF=OC•OE；
（2）若点F是DC的中点，联结BD交AE于点G，求证：四边形EFDG是菱形．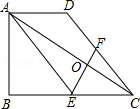
春季流感爆发，某校为了解全体学生患流感情况，随机抽取部分班级对患流感人数的进行调查，发现被抽查各班级患流感人数只有1名、2名、3名、4名、5名、6名这六种情况，并制成如下两幅不完整的统计图：
（1）抽查了 个班级，并将该条形统计图（图2）补充完整；
（2）扇形图（图1）中患流感人数为4名所在扇形的圆心角的度数为 ；
（3）若该校有45个班级，请估计该校此次患流感的人数．
如图，在△ABC中，AB=AC=10，sinC=
，点D是BC上一点，且DC=AC．
（1）求BD的长；
（2）求tan∠BAD．