(本小题10分)
某隧道的横段面是由一段抛物线及矩形的三边组成的,尺寸如图所示。某卡车空车时能通过此隧道。现载一集装箱,箱宽3米,车与箱共高 米。此时,卡车能否通过此隧道?说明理由。
米。此时,卡车能否通过此隧道?说明理由。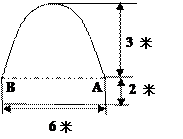
已知复数 ,(
,( ,
, 为虚单位)。
为虚单位)。
(1)若 为实数,求
为实数,求 的值;
的值;
(2)若复数 对应的点在第四象限,求实数
对应的点在第四象限,求实数 的取值范围
的取值范围
某工厂有A、B两种配件生产甲、乙两种产品,每生产一种甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天8h计算,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
已知函数 在点
在点 处取得极小值-4,使其导数
处取得极小值-4,使其导数 的
的 的取值范围为
的取值范围为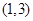 ,求:
,求:
(1) 的解析式;
的解析式;
(2) ,求
,求 的最大值;
的最大值;
已知: ,
, ,
, 是的内角,
是的内角, ,
,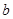 ,
, 分别是其对边长,向量,,.
分别是其对边长,向量,,.
(1)求角A的大小;
(2)若求的长.
如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90 ,BC=,求二面角S-AB-C的余弦值.
,BC=,求二面角S-AB-C的余弦值.