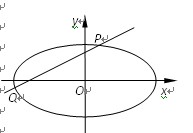
(本小题12分)已知函数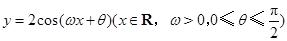 的图象与
的图象与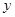 轴相交于点M
轴相交于点M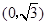 ,
,
且该函数的最小正周期为 .
.
(1)求 和
和 的值;
的值;
(2)已知点 ,点
,点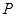 是该函数图象上一点,点
是该函数图象上一点,点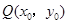 是
是 的中点,当
的中点,当 ,
,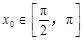 时,求
时,求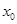 的值。
的值。
(本题满分14分) 如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB= ,AD=3,BB1=1.
,AD=3,BB1=1.
(Ⅰ) 设O是线段BD的中点,
求证:C1O∥平面AB1D1;
(Ⅱ) 求直线AB1与平面ADD1所成的角.
(本题满分14分) 设首项为a1,公差为d的等差数列{an}的前n项和为Sn.
已知a7=-2,S5=30.
(Ⅰ) 求a1及d;
(Ⅱ) 若数列{bn}满足an=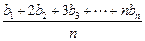 (n∈N*),
(n∈N*),
求数列{bn}的通项公式 .
.
(本题满分14分)在锐角△ABC中,cos B+cos (A-C)=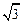 sin C.
sin C.
(Ⅰ) 求角A的大小;
(Ⅱ) 当BC=2时,求△ABC面积的最大值.
(本题满分14分) 已知实数a满足0<a≤2,a≠1,设函数f (x)= x3-
x3-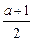 x2+ax.
x2+ax.
(Ⅰ) 当a=2时,求f (x)的极小值;
(Ⅱ) 若函数g(x)=x3+bx2-(2b+4)x+ln x (b∈R)的极小值点与f (x)的极小值点相同.求证:g(x)的极大值小于等于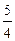 .
.
求a,b及c的值.
(本题满分15分)已知中心在原点O,焦点在x轴上,离心率为
 的椭圆过点(
的椭圆过点(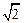 ,
, ).
).
(Ⅰ) 求椭圆的方程;
(Ⅱ) 设不过原点O的直线l与该椭圆交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的 取值范围.
取值范围.