（本小题满分12分）．已知椭圆的中心在原点，焦点在
轴上，离心率
，一
条准线的方程为
（Ⅰ）求椭圆的方程；（Ⅱ）设
，直线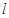
过椭圆的右焦点为
且与椭圆交于
、
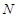两点，若
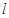，求直线的方程
已知f(x)＝2x，g(x)＝3－x2，试判断函数y＝f(x)－g(x)的零点个数．
已知函数f(x)＝x2＋ax＋b的两个零点是－2和3，解不等式bf(ax)>0；
(1)求函数f(x)＝x3－2x2－x＋2的零点；
(2)已知函数f(x)＝ln(x＋1)－
，试求函数的零点个数．
已知两条直线l1：y＝m和l2：y＝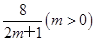
，l1与函数y＝|log2x|的图象从左至右相交于点A、B，l2与函数y＝|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时，求
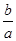的最小值．
已知函数f(x)＝lg(ax－bx)(a>1>b>0)．
(1)求函数y＝f(x)的定义域；
(2)在函数y＝f(x)的图象上是否存在不同的两点，使过此两点的直线平行于x轴；
(3)当a、b满足什么关系时，f(x)在区间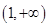
上恒取正值．