(本小题满分12分)
随着国家政策对节能环保型小排量车的调整,两款1.1升排量的Q型车、R型车的销量引起市场的关注.已知2011年1月Q型车的销量为 辆,通过分析预测,若以2011年1月为第1月,其后两年内Q型车每月的销量都将以1%的
辆,通过分析预测,若以2011年1月为第1月,其后两年内Q型车每月的销量都将以1%的 增长率增长,而R型车前
增长率增长,而R型车前 个月的销售总量
个月的销售总量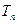 满足关系式:
满足关系式:
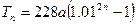
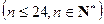 .
.
(Ⅰ)求Q型车前 个月的销售总量
个月的销售总量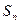 的表达式;
的表达式;
(Ⅱ)比较两款车前 个月的销售总量
个月的销售总量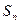 与
与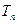 的大小关系;
的大小关系;
已知命题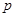 :“
:“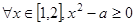 ”,命题
”,命题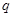 :“
:“ ”,若命题“
”,若命题“ ”是真命题,求实数
”是真命题,求实数 的取值范围。
的取值范围。
(本小题14分)已知函数 ,设
,设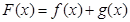 。
。
(Ⅰ)求F(x)的单调区间;
(Ⅱ)若以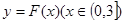 图象上任意一点
图象上任意一点 为切点的切线的斜率
为切点的切线的斜率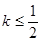 恒成立,求实数
恒成立,求实数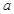 的最小值。
的最小值。
(Ⅲ)是否存在实数 ,使得函数
,使得函数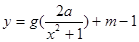 的图象与
的图象与 的图象恰好有四个不同的交点?若存在,求出
的图象恰好有四个不同的交点?若存在,求出 的取值范围,若不存在,说名理由。
的取值范围,若不存在,说名理由。
(本小题满分13分)已知中心在坐标原点O,焦点在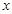 轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)
轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)
(Ⅰ)求椭圆的方程;
(Ⅱ)直线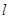 平行于
平行于 ,且与椭圆交于A、B两个不同点.
,且与椭圆交于A、B两个不同点.
(ⅰ)若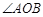 为钝角,求直线
为钝角,求直线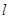 在
在 轴上的截距m的取值范围;
轴上的截距m的取值范围;
(ⅱ)求证直线MA、MB与x轴围成的三角形总是等腰三角形.
(本小题12分)已知数列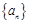 是各项均不为
是各项均不为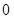 的等差数列,公差为
的等差数列,公差为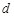 ,
, 为其前
为其前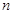 项和,且满足
项和,且满足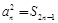 ,
, .数列
.数列 满足
满足 ,
,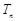 为数列
为数列 的前n项和.
的前n项和.
(Ⅰ)求数列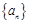 的通项公式
的通项公式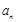 和数列
和数列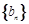 的前n项和
的前n项和 ;
;
(Ⅱ)若对任意的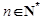 ,不等式
,不等式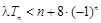 恒成立,求实数
恒成立,求实数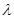 的取值范围;
的取值范围;
(本小题12分)在直三棱柱(侧棱垂直底面) 中,
中,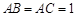 ,
, .
.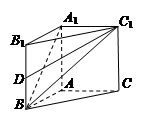
(Ⅰ)若异面直线 与
与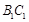 所成的角为
所成的角为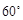 ,求棱柱的高;
,求棱柱的高;
(Ⅱ)设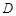 是
是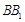 的中点,
的中点,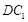 与平面
与平面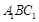 所成的角为
所成的角为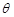 ,当棱柱的高变化时,求
,当棱柱的高变化时,求 的最大值.
的最大值.