(本小题满分13分)已知中心在坐标原点O,焦点在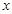 轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)
轴上,长轴长是短轴长的2倍的椭圆经过点M(2,1)
(Ⅰ)求椭圆的方程;
(Ⅱ)直线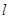 平行于
平行于 ,且与椭圆交于A、B两个不同点.
,且与椭圆交于A、B两个不同点.
(ⅰ)若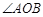 为钝角,求直线
为钝角,求直线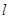 在
在 轴上的截距m的取值范围;
轴上的截距m的取值范围;
(ⅱ)求证直线MA、MB与x轴围成的三角形总是等腰三角形.
(本小题满分13分)已知数列 的前
的前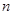 项和
项和 ,满足
,满足 为常数,且
为常数,且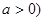 ,且
,且 是
是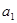 与
与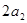 的等差中项.
的等差中项.
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列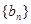 的前
的前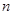 项和
项和 .
.
(本小题满分12分)如图,已知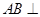 平面
平面 是正三角形,
是正三角形,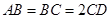 .
.
(Ⅰ)在线段 上是否存在一点
上是否存在一点 ,使
,使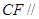 平面
平面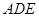 ?
?
(Ⅱ)求证:平面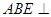 平面
平面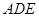 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
(本小题满分12分)已知抛物线 的顶点在坐标原点
的顶点在坐标原点 ,对称轴为
,对称轴为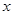 轴,焦点为
轴,焦点为 ,抛物线上一点
,抛物线上一点 的横坐标为
的横坐标为 ,且
,且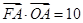 .
.
(Ⅰ)求此抛物线 的方程;
的方程;
(Ⅱ)过点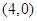 做直线
做直线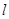 交抛物线
交抛物线 于
于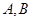 两点,求证:
两点,求证: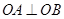 .
.
(本小题满分12分)已知命题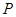 :在
:在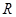 上定义运算
上定义运算 :
: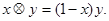 不等式
不等式 对任意实数
对任意实数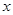 恒成立;命题
恒成立;命题 :若不等式
:若不等式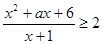 对任意的
对任意的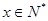 恒成立.若
恒成立.若 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围.
(本小题满分12分)在 中,角
中,角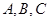 的对边分别为
的对边分别为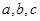 ,已知
,已知 .
.
(Ⅰ)求角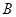 的大小;
的大小;
(Ⅱ)若 ,求△
,求△ 的面积.
的面积.