(本小题满分12分)已知抛物线 的顶点在坐标原点
的顶点在坐标原点 ,对称轴为
,对称轴为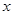 轴,焦点为
轴,焦点为 ,抛物线上一点
,抛物线上一点 的横坐标为
的横坐标为 ,且
,且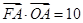 .
.
(Ⅰ)求此抛物线 的方程;
的方程;
(Ⅱ)过点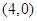 做直线
做直线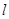 交抛物线
交抛物线 于
于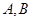 两点,求证:
两点,求证: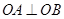 .
.
. (本题满分13分)
已知函数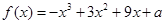
(1)求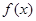 的单调递减区间;
的单调递减区间;
(2)若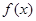 在区间
在区间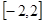 上的最大值为20,求它在该区间上的最小值。
上的最大值为20,求它在该区间上的最小值。
、(本题15分)已知函数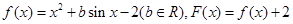 ,且对于任意实数
,且对于任意实数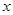 ,恒有F(x)=F(-x)。(1)求函数
,恒有F(x)=F(-x)。(1)求函数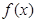 的解析式;
的解析式;
(2)已知函数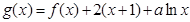 在区间
在区间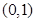 上单调,求实数
上单调,求实数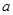 的取值范围;
的取值范围;
(3)函数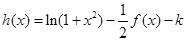 有几个零点?
有几个零点?
(本小题满分15分)已知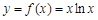 .
.
(1)求函数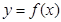 的图像在
的图像在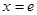 处的切线方程;
处的切线方程;
(2)设实数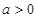 ,求函数
,求函数 在
在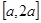 上的最大值;
上的最大值;
(3)证明对一切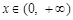 ,都有
,都有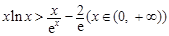 成立。
成立。
(本小题14分)已知函数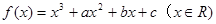 在
在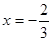 处取得极值,其图象在点
处取得极值,其图象在点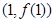 处的切线与直线
处的切线与直线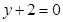 平行(1)求
平行(1)求 的值;
的值;
(2)若对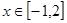 都有
都有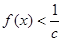 恒成立,求
恒成立,求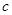 的取值范围。
的取值范围。
(本小题14分)已知函数f(x)=3x,且f(a+2)=18,g(x)=3ax-4x的定义域为区间[-1,1].(1)求g(x)的解析式;(2)判断g(x)的单调性.