已知斜三棱柱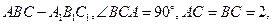
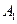 在底面
在底面 上的射影恰为
上的射影恰为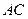 的中点
的中点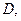 又知
又知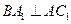 ;
;
(1)求证 :
: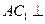 平面
平面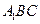 ;
;
(2)求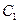 到平面
到平面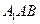 的距离;
的距离;
(3)求二面角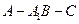 的余弦值;
的余弦值;
年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人,他们的健康状况如下表:
| 健康指数 |
2 |
1 |
0 |
﹣1 |
| 60岁至79岁的人数 |
120 |
133[] |
34 |
13 |
| 80岁及以上的人数 |
9 |
18 |
14 |
9 |
其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,﹣1代表“生活不能自理”.
(1)随机访问该小区一位80岁以下的老龄人,该老人生活能够自理的概率是多少?
(2)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率.
在△ABC中,角A,B, C所对的边分别是a,b,c,已知c=2,C= .
.
(1)若△ABC的面积等于 ,求a,b;
,求a,b;
(2)若cosA= ,求b.
,求b.
已知函数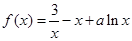 ,且
,且 是函数
是函数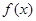 的一个极值点.
的一个极值点.
(1)求 的值;
的值;
(2)求函数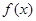 的单调区间;
的单调区间;
(3)设 ,当函数
,当函数 在区间
在区间 上零点的个数为0个,3个时,实数
上零点的个数为0个,3个时,实数 的取值范围分别为多少?(参考数据:
的取值范围分别为多少?(参考数据: ,
, )
)
若等比数列{ }的前n项和为
}的前n项和为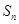 ,已知对任意的
,已知对任意的 ,点
,点 ,均在函数
,均在函数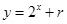 (
(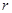 为常数)的图像上.
为常数)的图像上.
(1)求 和
和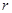 的值;
的值;
(2)记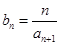 ,求数列
,求数列 的前
的前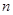 项和
项和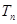
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB。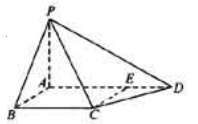
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD= 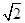 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积